CONTENTS Passive Properties
Nernst equation: Equilibrium and reversal potential Goldman equation: Goldman-Hodgkin-Katz constant field equation Pumps: Na/K exchange pump Permeability vs Conductance
Basic RC properties Input resistance Membrane time constant Low-pass filter
Attenuation and delay: Basic cable properties Space (length) constant: : Attenuation with distance Time constant: Time delay with distance Input resistance Non-uniform diameter: A compartmental model Spatial summation
Units: Passive property units Action Potentials (Spikes) Spike Conceptual Summary
Threshold: All-or-none? Sodium Dependence Hyperkalaemia: Too much extracellular potassium Spike Currents and Conductance Molecular Events: Single-channel patch recording Strength-Duration Curve Refractory Period Threshold Accommodation Rebound Excitation: Post-inhibitory rebound Pacemaker: Continuous regular spiking
Basic Conduction Features Collision Spatial Distribution: Voltage profile along the axon Passive vs Active Conduction: A qualitative comparison Refractory Conduction Myelination and Saltatory Conduction
Theory Classic HH: How to get a Nobel prize Sodium IV Curve Potassium IV Curve Capacitive Current: Importance in voltage clamp mechanism Patch Recording: Single channel recording under voltage clamp
Endogenous Bursters Plateau Potentials A Current: Fast (transient) potassium current
Gate Voltage Dependency Channel Voltage Dependency Putting it Together: Finding the membrane potential Non-Ohmic Channels: The GHK current equation Reduced Models: Morris-Lecar and others Phase Plane Analysis
Synapses
Excitation and Inhibition Voltage Clamp: Applied to synaptic potentials Summation and Facilitation Depolarizing and Silent IPSPs Non-Spiking Synapses Voltage-Dependent Synapses: NMDA-type Hebbian Synapses: The basis of memory? Quantal Release
Frequency Matters Size Matters Rectification
Proximal and Distal Inhibtion Directional Sensitivity
Networks
Flip-Flop Circuit Reciprocal Inhibition Oscillator Multi Phase Rhythms Sensory Feedback Phase Resetting Tests Tadpole Swimming: A case study Synchronization and Entrainment
Stochastic Resonance: Noise matters Lateral Inhibition
Primary Afferent Depolarization (PAD)
Phase Ambiguity
Classical Conditioning: Pavlov's dog Associative Learning: Pattern completion Facilities for Memory Models
Theory: Population-level coding in the Wilson-Cowan model Neurosim Implementation Stable States Oscillations Multi-Unit Models
Single-Channel Kinetics
Sojourn Duration and Transition Rate Constants Sojourn Distribution is Exponential
Open-Time Distribution Closed-Time Distribution is Multi-Exponential
What's the Point?: A reminder
Open-Time Distribution Closed-Time Distribution
Acetylcholine Receptor Model Auto-Correlation Compartmental Models Active Currents Neurosim Implementation Implementation
Passive Properties Noise Spiking Properties Voltage-Dependent Channels Ca-Dependent Channels Sodium Pump
Spiking Chemical Synapses Non-Spiking Chemical Synapses Carrier Ions: Calcium and sodium Electrical Synapses
Exponential Euler Integration Integration Components Adaptive Step Size Wilson-Cowan integration
References
$\setCounter{50}$
Contents

Copyright © W. J. Heitler (2019)

Synapses

Synapses are the communication nodes of the nervous system. They are the sites where one neuron passes on information to another neuron, or to an effector organ such as a muscle. So synapses enable the nervous system to make an animal actually do something - to behave. However, synapses not only transmit information, they also enable neurons to integrate that information and make decisions based on it (to spike or not to spike). Essentially, it is synapses that enable the brain to think. So synapses are important.

This chapter describes simulations concerning the post-synaptic electrical events that occur at:

 

Chemical Synapses

At a chemical synapse, information is transmitted between neurons in the form of a chemical signal. Specifically, depolarization in the output region of a pre-synaptic neurone opens voltage-dependent calcium channels, and the resulting inflow of calcium triggers the exocytosis of vesicles containing the chemical signal, the neurotransmitter. This diffuses across the synaptic cleft and interacts with receptors on the post-synaptic membrane. It is this interaction which causes electrical events in the post-synaptic neuron.

In a spiking chemical synapses only a spike in the pre-synaptic neuron generates enough depolarization to cause transmitter release. In a non-spiking chemical synapses, sub-threshold pre-synaptic depolarization can cause transmitter release on its own, without the occurrence of a spike.

Excitation and Inhibition

Three neurons are visible as yellow blobs in the Setup view. A line ending in a blue diamond runs from N1 to N3; this represents a synaptic connexion. A similar line runs from N2 to N3. The diamond shape shows that the synapses are of the spiking chemicalNon-spiking chemical synapses are shown as rounded-rectangles, and electrical synapses are shown as squares. type, and the labels a and b indicate that they have different propertiesNote that the synapse labels a and b are arbitrary. They indicate that they are different types of synapses with different properties, but they have no meaning outside the program. Synapse propertes are set using the Synapses menu command.. N1 and N2 are both stimulated with positive current (square boxes 1 and 2) and spikeThe neurons in these simulations are modelled using an integrate-and-fire algorithm. This means that the spikes are just digital events that trigger synaptic output, they are not implementing the HH equations. This is much faster, but it means that the appearance of the spikes in the Results view is just cosmetic. in response, generating post-synaptic potentials (PSPs) in N3.

In the Results view we see the membrane potentials of the 3 neurons, plus a stimulus monitor under each one.

Question: One of the synapses generates an excitatory post-synaptic potential (EPSP) in N3 while the other generates an inhibitory post-synaptic potential (IPSP). Which is which?

Does the outcome confirm your ideas regarding EPSPs and IPSPs?

These synapses require spikes in the pre-synaptic neuron to trigger transmitter release. This is not always the case, as we will see shortly.

We have now injected a stimulus into N3 to raise its membrane potential during the time of the PSPs. You should see that the EPSPs have got smaller in terms of their base–to-peak height, while the IPSPs have got bigger.

Now the EPSPs have got bigger. The IPSPs, however, have reversed their direction. Instead of going negative from their base potential, they go positive!

Question: Why do the PSPs change in base-to-peak amplitude, and why do the IPSPs reverse polarity with hyperpolarization? You can assume that the conductance change underlying the PSPs is not affected by the post-synaptic membrane potential. Hint: Think about equilibrium potentials and driving force.

Integration

In a real nervous system, an individual post-synaptic neuron may receive input from manyPerhaps up to 1000 different pre-synaptic neurons, some of which is excitatory and some inhibitory.

Again we have a post-synaptic neuron (N1, blue) receiving excitatory and inhibitory synaptic input, but this time there are 6 excitatory neurons (e2 - e7, red) and 6 inhibitory neurons (i8 - i13, green) pre-synaptic to N1. The pre-synaptic neurons each receive a tonic, randomly-varying stimulus current which makes them spike at random intervals, and thus deliver EPSPs and IPSPs to the post-synaptic neuron. Due to the random nature of the stimulus current, the spike pattern will vary with each simulation run. The strength of each synapse has itself been randomized (see the Connections: Randomize menu command), meaning that each synaptic connection varies in the strength of the input it makes to N1.

The Spike Frequency dialog shows a bar graph of the cumulative spike frequency of each neuron. The post-synaptic neuron, N1, is the left-most column in the chart. N1 receives an about equal balance of excitation and inhibition, and spikes at about the same frequency as the pre-synaptic neurons themselves.

Note that without inhibition the frequency of post-synaptic spikes increases considerably; it is now about twice the frequency of the pre-synaptic neurons. This is apparent both from the density of spikes in the top trace in the Results view, and from the height of the bar in the N1 column of the Spike Frequency dialog.

Now the post-synaptic neuron N1 never spikes, because it only receives inhibitory synaptic input.

Take-home message: The post-synaptic neuron integrates its synaptic inputs (essentially sums them together), and if the resulting membrane potential rises above threshold it generates a spike signal, which may then be passed on to other neurons. If the post-synaptic neuron does not spike, no signal is passed on. The propagation of a signal thus depends on the balance of excitation and inhibition in each neuron in a circuit.

Voltage Clamp

Ligand-gated (synaptic) channels can be examined under voltage clamp just like voltage-dependent channels. (A general description of the voltage clamp technique was given previously, and you could review it if you need a reminder.) The advantage of the voltage clamp technique is that it can directly reveal the currents underlying the PSPs, which in turn can allow the conductance to be calculated.

Despite the filename, the simulation starts in normal current clamp mode, so you see the voltage response in the post-synaptic neuron. As before, two pre-synaptic neurons are activatedThe activation times and synapse properties can be examined and specified by checking the Properties box in the Synapses group in the Setup view. and in this case generate a single spike each, but these are not visibleThis is because the simulation is using the Advanced HH module, which only shows one neuron. This module is needed because it implements the voltage clamp protocol, which is not available in the Network module.. They cause an EPSP followed by an IPSP in the post-synaptic neuron. Note: to keep things simple, in this simulation the post-synaptic neuron has no voltage-dependent channels (it is a non-spiking neuron). The only ion channels in the membrane are the leakage channels which generate the resting potential, and the ion channels underlying the two PSPs.

The upper trace shows the membrane potential, which is completely flat because the clamp potential is set the same as the holding potential, which is itself set to the unclamped resting potential of -60 mV.

The middle trace shows the total current generated by the voltage clamp, which mirrors the ionic current across the membrane. The initial clamp current is 0. This is because the membrane is clamped at the resting potential, and no clamp current is needed to maintain this voltage. However, 5 ms after the start of the run, the excitatory synapse is activated, and there is a downward deflection in the current trace reflecting the inward current flowing through the cholinergic receptor channels. The downward deflection is because the clamp has to inject negative current to prevent the positive current flowing through the open ion channels from shifting the membrane potential in a positive direction. A little later the inhibitory synapse is activated, and there is an upwards deflection in the clamp current trace counteracting the outward current flowing through the open GABA receptor channels.

The lower trace shows the conductance of the two types of channel generating the PSPs (EPSP red, IPSP green). Remember that these cannot be recorded directly in an experiment - they are calculated during the simulation from the underlying data.

One feature that is immediately obvious is that the current pulses (and underlying conductance changes) are much briefer than voltage change in the membrane potential seen in the initial experiment before the voltage clamp was applied. This is because the capacitance of the membrane slows down the voltage response to a current pulse (see the Basic RC Properties section if you want a reminder about this).

Question: Why are the current profiles for the two PSPs (middle trace) so different from each other in amplitude and direction, when the underlying conductance changes (bottom trace) are identical?

As soon as a depolarizing clamp step is applied, the current trace shows a step change upwards. This reflects the leakage current - the current needed to keep the membrane potential elevated above its natural resting potential. A little later, the synapses are activated and there is additional clamp current needed to counteract the current flowing through the open receptor channels.

Task: Find the equilibrium (reversal) potential for the EPSP. Hint: The clamp current during the PSP is made up of a combination of the leakage current and the synaptic current; these need to be separated to find the PSP equilibrium potential. This can be done by constructing separate I/V plots for the components. The following protocol reflects one commonly found in published research papers.

The graph below shows the expected outcome of the task:

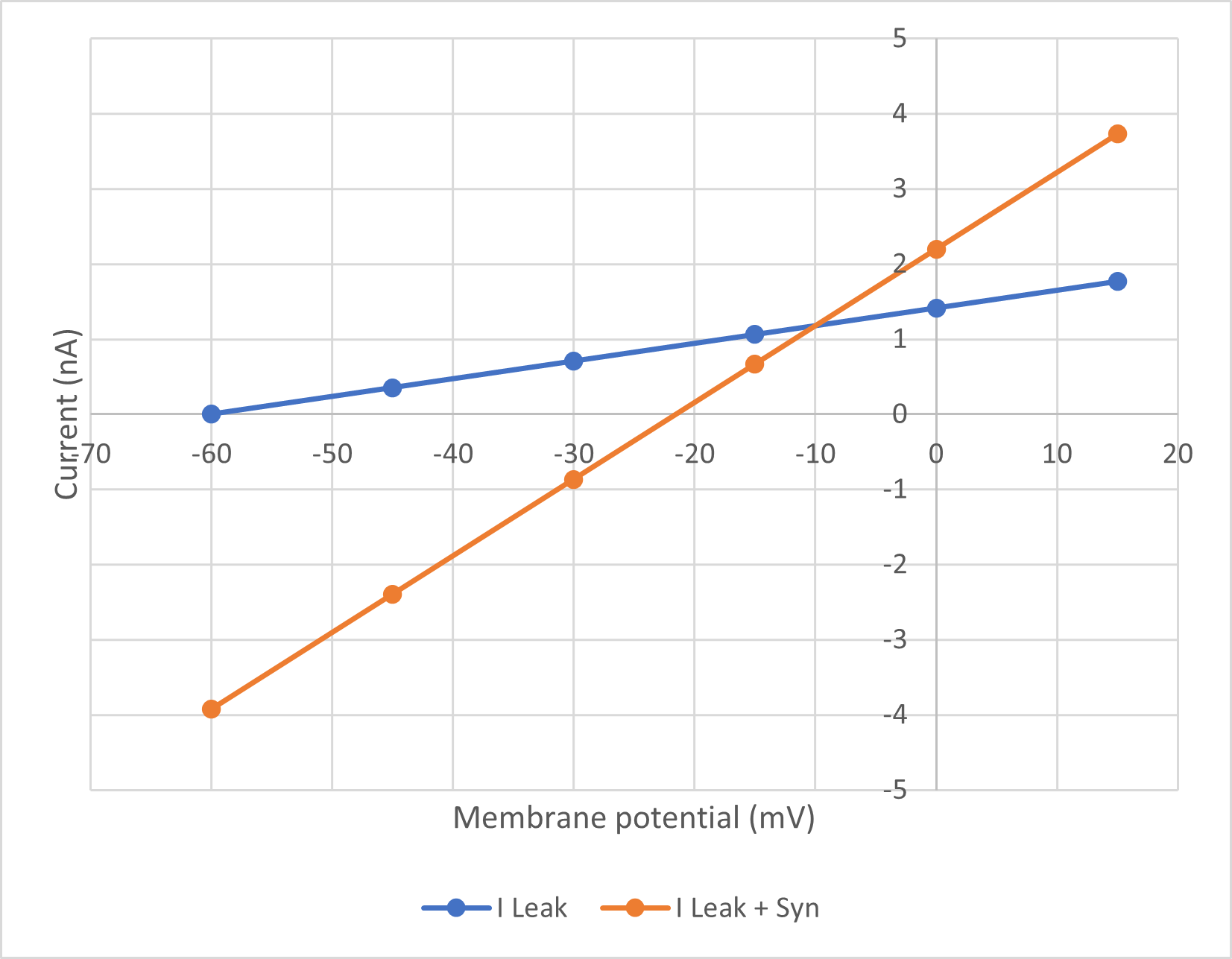
Synapse I/V curve

Synapse equilibrium potential. I/V plots for the leakage current and the leakage + synaptic current are shown superimposed. The equilibrium potential for the synaptic current is where the lines intersect.

The blue line is the leakage current on its own (IL), the orange line is the combined leakage and synaptic current (IL + IS). Where the lines intersect the two are equal, so the synaptic current is zero (if IL = IL + IS, then IS = 0). The voltage at which this occurs is thus the equilibrium potentialThis follows from the driving force equation I = g(Em - Eeq). We can assume that g is non-zero, because there is synaptic current at voltages on either side of the intersect (IL ≠ IL + IS). So if I is zero but g is non-zero, Em - Eeq must be zero, meaning Em = Eeq. for the synaptic current.

Question: What is the equilibrium potential for the IPSP?

Hint: You could use the same approach as for the EPSC, but for this simulation there is a simpler way. You can just note the clamp potential at which the current trace is a flat line - i.e. the clamp current at the peak of the inhibitory conductance is equal to the leakage current. This is possible because the equilibrium potential just happens to exactly match one of the voltage clamp steps!

Summation and Facilitation

The Setup view shows is a simple circuit in which N1 makes an excitatory synapseThe synapse label is again a, but the properties are different from the previous a. As stated earlier, the label IDs are arbitrary onto N2. N1 is driven to spike at quite high frequency by a train of brief stimuli (look at the stimulus 1 parameters). The EPSPs increase in peak amplitude as the train progresses.

Question: Do the EPSPs show summation, facilitation, or both?

Remember that summation is a post-synaptic phenomenon, when the voltage change produced by closely-spaced EPSPs sum with each other, whereas facilitation is a pre-synaptic phenomenon, in which successive spikes release greater amounts of transmitter.

The stimuli to N1 now occur at lower frequency, and the EPSPs in N2 are more separated in time. Does this affect your answer to the previous question?

Depolarising and Silent IPSPs

At first site, the synapse looks like it is generating EPSPs, but in fact, the response is inhibitory despite the fact that it is depolarising.

Note that the PSPs that looked like EPSPs now look like IPSPs!

The stimulus is now big enough to generate spikes in the post-synaptic neuron, and you can see that the IPSPs interrupt the spike train, thus showing that even though they are depolarising when the post-synaptic neuron is at rest, they are none-the-less really inhibitory.

This type of depolarising inhibition is quite common, especially in pre-synaptic inhibition. It usually arises from an increased chloride conductance when the chloride equilibrium potential is depolarised relative to the resting potential.

Hyperpolarizing IPSPs inhibit neurons through two mechanisms. First they simply take the membrane potential further from threshold, so it takes more excitation to generate a spike. But secondly, they have a “shunting” effect. This means that the increase in conductance that generates them will tend to short-circuit any excitatory currents that are generated by nearby concurrent EPSPs.

Depolarizing IPSPs lack the first mechanism, but they certainly include the second. They may also have an additional property that can make them even more effective. The small depolarization that they generate can activate voltage-dependent potassium channels, and start to inactivate sodium channels. They thus effectively render the patch of membrane where they occur somewhat refractory, thus reducing the probability of it generating a spike. This is similar in principle to spike threshold accommodation, which you may have seen earlier.

Take-home message: A PSP may generate a depolarizing potential when activated at the resting potential of the post-synaptic neuron, but that does not of itself tell you whether it is excitatory or inhibitory.

Absolutely nothing seems to happen in the post-synaptic cell, despite the pre-synaptic spikes.

Now IPSPs are clearly apparent!

The explanation here is that the synapse generates an increase in chloride conductance in the post-synaptic neuron (N2), but the chloride equilibrium potential is the same as the resting membrane potential. Therefore the driving force is zero and there is no current, and hence no voltage change. However, as soon as you perturb the membrane potential to take it away from the chloride equilibrium potential, the PSPs are revealed.

Non-Spiking Synapses

Transmitter release from the pre-synaptic terminal is triggered by an inflow of calcium through voltage-dependent calcium channels. In many neurons, these channels have a high threshold, and only a spike invading the pre-synaptic terminal can depolarize it enough to open the channels and cause transmitter release. However, in some neurons the calcium channels have a low threshold, and transmitter can be released just by depolarizing the terminal without generating a spike. Indeed, in some neurons transmitter is released even at resting potential, and its release can be modulated by any change in potential in the pre-synaptic neuron.

Nothing appears to happen.

N1 connects to N2 through a non-spiking chemical excitatory synapse. The properties are similar to those of the nicotinic acetylcholine synapse, but in this case transmitter release from the pre-synaptic neuron does not require spikes. Instead, transmitter is released in a graded manner, with increased pre-synaptic depolarisation leading to increased release of transmitter, up to a saturation level.

Note that for the first few stimuli, both N1 and N2 hyperpolarize. But then, while N1 continues to hyperpolarize, N2 does not.

Question: Why does N2 hyperpolarise at all? Why does the N2 hyperpolarisation not increase beyond a certain level as you increase the hyperpolarisation of N1? Hint: think about turning off a dripping tap.

Non-spiking synapses are not obscure oddities. In fact, if you are reading this tutorial, you are using them right now. The rods and cones of the vertebrate retina do not generate spikes, but release transmitter at a level determined by their membrane potential. They are depolarized in the dark and continuously release transmitter, and this release is reduced by light-activated hyperpolarization.

Voltage-Dependent Synapses (NMDA-type)

Some post-synaptic receptors at chemical synapses have a voltage-dependent conductance. The classic example is the NMDAN-methyl-D-aspartate-receptor. The natural agonist for this is glutamateThe receptor also requires glycine or D-serine to bind to it for full activation., but glutamate can also activate a variety of other receptors. A highly specific artificial agonist is NMDA, from which the receptor derives its name.

The voltage-dependency results from magnesium block. At the normal resting potential, magnesium ions, which are naturally present in the extracellular fluid, partially block the channel at resting potential. A magnesium ion literally plugs the channel, fitting into the channel lumen from the extracellular side. As the post-synaptic neuron depolarises, the positively-charged magnesium ions are increasingly expelled from the channel, thus relieving the block. This means that as the neuron depolarizes, the overall conductance of activated NMDA channels increases. The depolarization needed to remove the magnesium will reduce the driving force on the normal carrier ions (sodium and calcium), but usually not enough to significantly reduce their current.

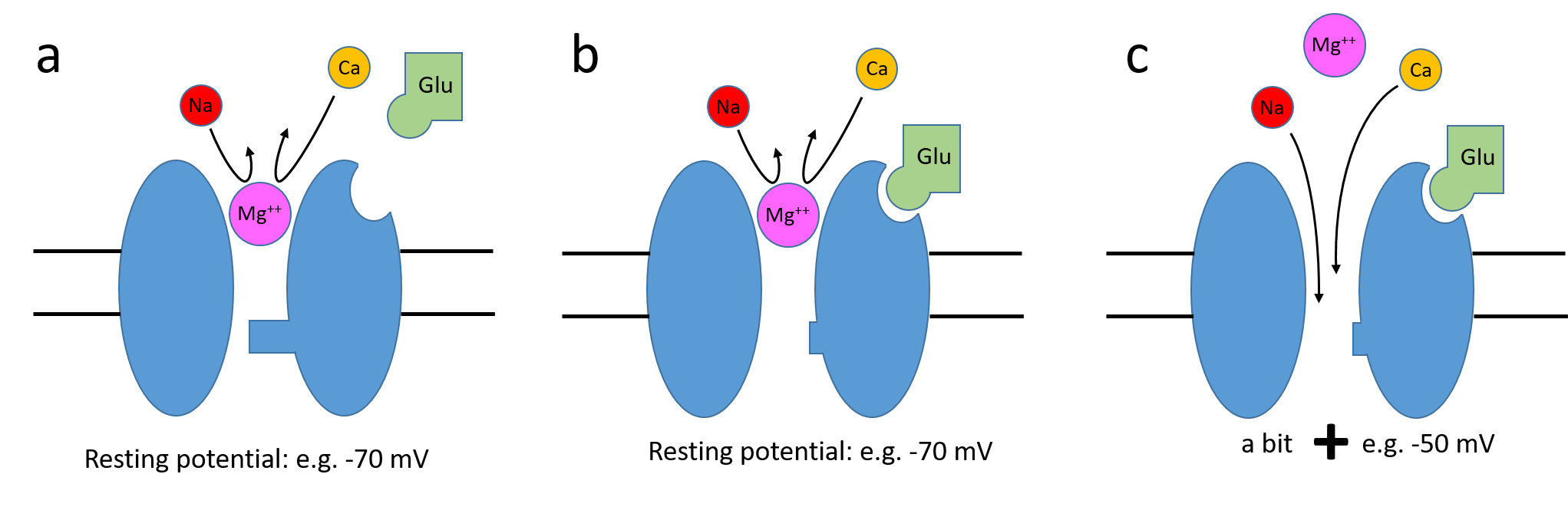
NMDA receptor
NMDA receptor. a. At rest and with the agonist unbound.The channel is shut and blocked. b. At rest but with the agonist bound. The channel is activated, but still blocked by magnesium. c. With slight depolarization the magnesium is expelled, and the activated channel is now open.

This looks just like the excitatory synapses that we have seen earlier.

Note that the size of the EPSP has increased! This is not what is expected for a normal excitatory PSP. Depolarizing the post-synaptic neuron takes its membrane potential closer to the equilibrium potential for an excitatory synapse, and thus the driving force decreases and the size of the EPSP should decrease. But in this case it increases.

The significance of this is that NMDA-receptor mediated responses have a tendency to self-reinforcement; as the synapse becomes more active (due to increased frequency of pre-synaptic spiking), the effectiveness of transmission is increased in a non-linear fashion, so that the post-synaptic cell rapidly depolarises to a higher potential level.

The pre-synaptic neuron now produces multiple spikes, and the summation of the EPSPs triggers the voltage-dependent increase. The post-synaptic cell "flips up" to a more depolarised level as the EPSPs summate to a level that removes the magnesium blockade, and then increase in amplitude.

NMDA I/V Curve

It may be instructive to look at the I/V curve for an NMDA-receptor mediated synapse: i.e. the relationship between post-synaptic synaptic current and post-synaptic voltage. To do this we need to run an experiment in voltage clamp mode.

As before, we use the Advanced HH module to do voltage clamp experiments, and this only shows the post-synaptic neuron. A pre-synaptic neuron (not visible) spikes at about 15 ms into the run, and generates an NMDA-mediate EPSP in the post-synaptic neuron seen in the Results view. To keep things simple, this post-synaptic neuron has no voltage-dependent channels (it is a non-spiking neuron) - the only ion channels in the membrane are the leakage channels which generate the resting potential, and the ion channels generating the EPSP.

We start off in standard current-clamp mode, just to confirm the general voltage-dependency.

Note that the paradoxical increase in the EPSP amplitude is similar to that seen in the previous simulation.

The upper trace shows the membrane potential, which is completely flat because the clamp potential is set the same as the holding potential, which is itself set to the unclamped resting potential of -60 mV.

The middle trace reflects the current flowing through the synaptic channels. In a real experiment this would have to be obtained by measuring the total current, and then subtracting the leakage current to obtain the synaptic current (although in this starting condition, the clamp potential is equal to the resting potential and so the leakage current is zero), but in a computer simulation we can do the subtraction automatically and display the synaptic current directly.

The lower trace shows the conductance of the synaptic channels generating the EPSP. As stated before (frequently) this cannot be recorded directly in a real experiment - it has to be calculated from the driving force equation.

Note that there is an increase in the synaptic current and the conductance. The conductance change is caused by the partial unblocking of the NMDA receptor channel, as magnesium ions are expelled from the extracellular lumen of the channel. The increased conductance causes an increased current.

Task: Construct an I/V plot showing how synaptic current varies with clamp potential, using the following procedure:

You should now see a J-shaped curve which is very similar to the I/V curve produced by voltage-dependent sodium channels. This is not a coincidence - both channels have the region of negative slope conductance characteristic of regenerative processes that can cause a rapid, spike-like depolarization. Look back at the sodium experiment if you want a reminder about this.

Question: What is the approximate equilibrium potential of the NMDA response?

You know the synaptic current at each potential from the voltage clamp data, and you know the equilibrium potential from the I/V curve, so you could now calculate the conductance at each potential using the driving force equation. However, Neurosim does this for you, and displays the results in the conductance trace. Furthermore, you will have picked up the value of eachImp peak conductance when you measured the current.

Task: Construct a plot showing how conductance varies with membrane potential. This is extremely simple - just select G syn from the Y axis drop down list in the XY Scatter dialog (G is the standard symbol for conductance).

Question: At what membrane potential is the magnesium blockade fully relieved - i.e. what is the membrane potential that expels all the magnesium ions from all the channels?

Hebbian Synapses

An early theory of learning (devised by a man called Hebb, hence the name) was that learning occurred as a result of changes in synaptic strength, which depended upon the “conjoint firing” of pre- and post-synaptic neurons (Hebb, 1949). Hebbian synapses are synapses whose strength is increased when the pre- and post-synaptic neurons are active together. In its simplest form this means that when an excitatory Hebbian synaptic input is “successful” in eliciting a spike in the post-synaptic neuron, the synapse gets strengthened. This means that the synapse is likely to be more effective the next time it is activated. Conversely, if the Hebbian excitatory synaptic input is not followed by a spike in the receiving neuron, then the connexion does not get strengthened, or can even get weakened.

N1 spikes at constant low frequency (due to synaptic input from an unspecified neuron) and puts small EPSPs onto N2. In the middle of the sweep N2 is induced to spike by an injected current pulse (this could be a synaptic input from some other neuron). After the N2 spike, the synaptic input from N1 is much enhanced - thus when the N1-N2 connexion was "successful" (due to help from the stimulus) it got stronger. Note that the synapse in the Setup view is colour-coded according to its strength.

Notice that as time passes after the Hebbian effect, the enhanced response diminishes back to its starting state. The synapse has “forgotten”.

If the manual stimulus generates a spike in N2, it causes another enhancement of the EPSP.

At this stage, the post-synaptic neuron spikes in response to each EPSP and so the synapse receives reinforcement on each input and thus maintains the enhanced response, even with no further injected pulses. The synapse has “remembered” its reinforcement.

The post-synaptic spike is an essential feature to trigger Hebbian synaptic enhancement, and yet the enhancement itself may well involve the increase in transmitter release from the pre-synaptic neuron. This implies the once-heretical notion of a retrograde transmitter. This means that the post-synaptic neuron releases some substance when its activity level increases that has an effect back across the synapse specifically onto the active pre-synaptic terminal.

There is as yet no direct evidence that any real synapse displays Hebbian properties which are as simple as those in this simulation. However, Hebbian-type mechanisms may well underlie some of the important forms of learning which occur in the nervous system, such as long-term potentiation (LTP) and classical conditioning.

Quantal Release

At the heart of our modern understanding of chemical synapses is the concept of quantal release – the notion that transmitter is released in fixed-size packages, now known to be vesicles, from a pool of available vesicles, and that the number of vesicles released can vary. Katz and co-workers (del Castillo & Katz, 1954) established this in a series of classic papers that match the Hodgkin-Huxley papers in their influence, and which also led to a share in the Nobel prize for Katz.

This simulates a classic experiment. A neuron makes a connection to another neuron via a cholinergic synapse. The pre-synaptic neuron is stimulated repeatedly at a fixed frequency of 50 Hz, and the post-synaptic response is recorded. The Setup and Results views only show the post-synaptic neuron (the simulation is running in the module Advanced HH), and the pre-synaptic neuron is not shownThe pre-synaptic stimulus frequency and the synaptic properties are set in the Synapse Properties dialog box. If you wish, you can access this by checking the Properties box in the Synapses frame of the Setup view, but you don’t need to for this activity..

There is obviously some variation in the size of the EPSPs, but it is hard to see any obvious pattern.

The size of the EPSPs reduces substantially. This is because transmitter release is calcium-dependent.

You might notice two things:

First, there are occasional “gaps” in the response. The pre-synaptic neuron is spiking at a constant frequency (you have to just believe that – it is part of the simulation), but quite frequently it fails to elicit a response in the post-synaptic neuron.

Second: the size of the EPSP varies in relatively fixed steps, although because there is some noiseNoise, in this context, means random fluctuations in the signal that carry no useful information. in the recording (added intentionally in the simulation) the steps are not always absolutely equal.

The latter property can be seen more clearly as follows:

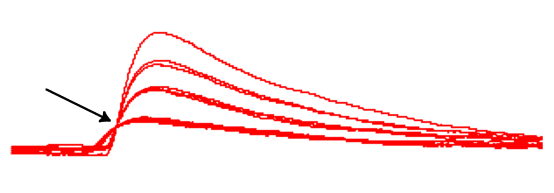
You are now seeing an expanded view of the individual PSPs that occur over the same time period (400 ms), but the PSPs are all lined up and superimposed. This is what is meant by “triggered”. The display sweep is synchronized to the time when the membrane potential crosses a user-specified Trig level (-59 mV in this case), and this happens on the rising front of the EPSPs. The display also captures some Pre-trig signal (set at 2 ms) so you can see the baseline activity just before the EPSP. This is standard display methodology frequently used in real experiments.

It should now be obvious that the size of the EPSPs is not continuously graded. Instead, EPSPs cluster into discrete size classes:

Quantal release steps
Quantal steps.The arrow shows the Neurosim Trigger level, which is the synchrony point where all the traces cross each other.

You should now see rather more steps in the EPSP amplitude.

The size of the EPSP is still clearly changing in steps, but there are (probably) none of the really small EPSPs visible. You may also start to see some slowly declining traces that are obviously not EPSPs. These are caused by trigger-crossing due to noise on the falling edge of the EPSP and can be ignored.

The data can be interpreted as follows. There is a pool of releasable vesicles in the pre-synaptic terminal, and with each pre-synaptic spike a random number of these are released, with the number fluctuating around some average value (the average quantal content). In reduced calcium, this average is reduced.

At the frog neuromuscular junction, where these experiments were first carried out, at normal levels of extracellular calcium, the average quantal content (average number of vesicles released per stimulus) is high, so transmission is very reliable. However, in synapses in the central nervous system, the average quantal content may be only 1 or 2, so pre-synaptic spikes frequently produce no post-synaptic response at all, because no vesicles are released.

Quantal Size Distribution

You should only read this is you are interested in the statistical properties of quantal release.

Assume that the total number of quanta available for release is n, and that the probability of any one quantum being released in response to a single pre-synaptic spike is p. This means that the average quantal content of an EPSP, m, will be equal to np. The probability P(k) of k quanta in total being released for a particular stimulus is given by the binomial distribution:

\begin{equation} P(k) = \frac{n!}{k!(n-k)!}p^k(1-p)^{n-k} \label{eq:eqBinomial} \end{equation}

The problem with this formulation is that although we can measure m experimentally (the average size of the PSPs divided by the minimum size), we cannot measure n or p, and so if we detect a change in m we do not know whether the effect has been mediated by changing the probability of release (p), or the number of quanta available for release (n).

One of the useful characteristics of the binomial distribution, is that if m is low compared to n, the distribution simplifies to a Poisson distribution 

\begin{equation} P(k) = \frac{m^k e^{-m}}{k!} \label{eq:eqPoisson} \end{equation}

This is still a bit of a mouthful, but the key point is that there are no unmeasurable quantities in the equation, and the releasable pool variable n doesn’t come into it. So any change in m that may occur means that p has changed, rather than n.

In order to use the simple Poisson equation, we need to be sure that quantal release follows a Poisson, rather than a binomial, distribution i.e. that m (the average number of quanta released) is small compared to n (the total number of quanta available for release). Happily, there is a fairly simple test we can apply.

When we stimulate the pre-synaptic neuron it sometimes fails to release transmitter at all, i.e. the quantal content is 0. We can measure the probability of this happening as simply the fraction of the total number of stimuli which fail to evoke EPSPs, i.e. the number of failures, N0, divided by the number of trials N. From the Poisson distribution above we know that:

\begin{equation*} P(0)=\frac{N_0}{N} = \frac{m^0e^{-m}}{0!} \end{equation*}

m0 and 0! are both 1, so this resolves to

\begin{equation*} N_0 = Ne^{-m} \end{equation*}

and hence

\begin{equation} m = \ln\frac{N}{N_0} \label{eq:eqQuantalM} \end{equation}

It was this sort of analysis that led to the conclusion that facilitation was usually due to an increase in the mean quantal content (m) of transmission.

 

Electrical Synapses

Electrical synapses are mediated by gap junctions that form an electrically-conducting cytoplasmic bridge from one neuron to another. This means that current can flow intracellularly between neurons. This has two important consequences. First, electrical synapses are faster than chemical synapses because they do not involve the intermediary chemical signal. Second, most electrical synapses can “share” both excitation and inhibition between pools of neurons, thus tending to synchronize them.

N1 and N2 are connected by an electrical synapse (the square synapse symbol in the Setup view). The synapse icon might suggest that N1 is anatomically pre-synaptic to N2, but that is just for consistency in the Setup layout, it does not represent the physiology.

First a pulse of positive current is injected into N1, where it produces a subthreshold depolarization. This spreads through the electrical synapse into N2, where it produces a somewhat smaller depolarization. So in this situation, N1 is presynaptic to N2. Second, a pulse of positive current is injected into N2, where it also produces a sub-threshold depolarization, which spreads to N1. So in this situation N2 is presynaptic to N1. The terms pre- and post-synaptic are thus operationally defined at this type of synapse - whichever is the source of the current is the pre-synaptic neuron, and this can change on a moment-by-moment basis.

The standard way to quantify the strength of an electrical synapse is to measure the coupling coefficient (Cf), which is simply the ratio of the post-synaptic voltage change (Vpost) to the pre-synaptic voltage change (Vpre). This relates to the synaptic and membrane conductance as follows:

\begin{equation} Cf = \frac{\Delta V_{post}}{\Delta V_{pre}} = \frac{g_s}{(g_s + g_{post})} \label{eq:eqCouplingCoefficient} \end{equation}

where gs is the synaptic conductance and gpost is the membrane conductance (reciprocal input resistance) of the post-synaptic neuron. (Note that the coupling coefficient is thus independent of the pre-synaptic membrane conductance. This conductance relationship can be shown by applying Ohm’s law, but I will not prove that here.)

Task: Measure the coupling coefficient for both stimuli, using the appropriate voltage values from the two neurons. To make it (marginally) more interesting, the two current pulses do not have quite the same amplitude. Hint: don't forget that it is the change in membrane potential that we are interested in.

The electrical synapse conductanceThis can be viewed in the Electrical Synapse Types dialog, which is accessed through the Synapses: Electrical menu command. is 10 nS, and the membrane conductanceThis can be viewed in the Neuron Properties dialog, which is accessed by right-clicking a neuron in the Setup view. of each neuron is 15.7080 nS. Does your measured coupling coefficient fit with these values?

NEM (n-ethylmaleimide) is a drug that blocksAt least in some types of tissue. It is not absolutely reliable. gap junctions.

Two changes are apparent. There is no longer a PSP in either neuron in response to the current injected into the other. That’s because the drug worked. Also, N1 starts to spike. [The simulation is using integrate-and-fire dynamics, so the spikes are not full HH types].

Question: Why does N1 spike when you add NEM? (And why doesn’t N2?) This is a slightly trick question in that it relies on the exact parameters of this simulation, so it is not a general principle. But it is worth considering because the answer helps firm-up understanding of what is happening at these synapses.

Take-home message: Simple electrical synapses are bidirectional and non-polarized. Current of either polarity will spread from either neuron to the other. This is in obvious contrast to chemical synapses, which normally mediate one-way information transfer from the pre- to the post-synaptic neuron.

Frequency Matters

Because of cell membrane capacitance, the coupling coefficient of an electrical synapse depends on the frequency of the signal being transmitted.

This is a bit complicated, but can be understood by going through it carefully.

There are two identical cell pairs, N1 + N2 (red, blue) and N3 + N4 (green, orange). The members of each pair are connected to each other by identical electrical synapses. N1, the top neuron on the left in the Setup view (red), is stimulated by a standard square pulse of current (stimulus 1). N3, the top neuron on the right (green), is stimulated by current that oscillates in a sine wave with a frequency of 50 Hz (stimulus 2).

In the Results view, the bottom axis shows the stimulating current applied to the two neurons. Note that the peak current for the oscillating (ACAC: alternating current. This is the term used when current varies with time. ) stimulus (green) is higher than that for the stable (DCDC: direct current. This is the term used when current is stable over time.) stimulus (red). The top axis shows the voltage responses of the two pre-synaptic neurons. They both reach the same peak amplitude (apart from the first cycle of the sine wave, which is larger due to the need for settling time).

Question: Why are there differences between the peaks of the AC and DC stimuli, when they both produce the same peak voltage response?

Hint: remember that due to its RCRC: resistor-capacitor properties the membrane acts like a low-pass filter.

The membrane potentials of the post-synaptic neurons, N2 (blue) and N4 (orange), are shown superimposed in the middle axis. Note that the voltage change in the post-synaptic neuron receiving oscillating input through the synapse (N4) is smaller than that receiving constant input (N2), even though the peak voltages in the pre-synaptic neurons are the same.

Note that the voltage response in the pre-synaptic cell (green trace, top axis) is delayed relative to the stimulus. The peak membrane voltage occurs after the peak stimulus current. This is a pre-synaptic phenomenon, and nothing to do with the electrical synapse.

Note that the peak of the post-synaptic response (orange trace, middle axis) occurs after the peak of the pre-synaptic signal, indicating a further phase delay introduced by the electrical synapse.

Take-home message: When transmitting a signal, electrical synapses attenuate and delay high frequency signals more than they do low frequency signals.

Size Matters

Although most electrical synapses are bidirectional and non-polarized, the relative size of electrically coupled neurons can have a strong functional influence.

N1 and N2 are connected to each other through an electrical synapse (square blue synapse), but N1 is bigger than N2 (100 µm in diameter compared to 50 µm). Both neurons receive an experimental current stimulus (square boxes 1 and 2).

Both N1 and N2 spikeThese spikes are generated using the HH equations. and their spikes are identical in size and shape. They each generate an electrical EPSP in their partner neuron, but these are very different in amplitude. The N2 EPSP (received by the small neuron from the large neurons, seen early in the blue trace, middle axis) is substantially bigger than the N1 EPSP (received by the large neuron from the small neuron, seen late in the red trace, top axis).

Take-home message: If a big neuron and a small neuron are electrically coupled, a spike in the big neuron makes a bigger EPSP in the small neuron than a spike in the small neuron makes in the big neuron. The synapse is effectively polarized.

The reason can be seen from the equation \eqref{eq:eqCouplingCoefficient} defining the coupling coefficient. A small post-synaptic neuron will have a lower membrane conductance (gpost) than a big neuron due to its reduced surface area, so the denominator in the equation is reduced and the coupling coefficient is bigger.

Rectification

Most electrical synapses are electrically symmetrical: they act as a simple low resistance path between the neurons. However, some electrical synapses are rectifying and act like an diode. The conductance (inverse resistance) of such a synapse depends on the trans-junctional potential, i.e. the difference in membrane potential between the two neurons. What this means in practice is that positive current will pass in one directionRemember that positive current flowing from A to B can be carried by positively charged ions such as K+ flowing from A to B, but it can just as easily be carried by negatively charged ions such as Cl- flowing from B to A. more easily than negative current, while negative current will pass more easily than positive current in the other. If the trans-junctional potential is such that the synapse is in the high conducting state, the synapses is said to be forwards biased. If it is in the low conductance state, it is reverse biased.

Two neurons are connected by a rectifying electrical synapse. The direction of rectification is from N1 to N2 (shown as a diode image in the Setup view). Four stimuli (the square boxes in the Setup view) are applied in sequence.

The first stimulus is positive current that depolarizes N1. It forward-biases the synapse, which moves into a high-conductance state, and the current flows from N1 into N2 and depolarizes it.

The second stimulus is negative current that hyperpolarizes N1. The synapse is reverse-biased and does not move into a high conductance state. Only a little current flows into N2, and the N2 response is weak. Note that the N1 response is actually bigger, because it is not “losing” so much current into N2.

The third stimulus is positive current that depolarizes N2. However, this is on the “wrong” side of the rectifier, so it reverse-biases the synapse, and little current flows into N1 and the N1 response is weak.

The fourth stimulus is negative current that hyperpolarizes N2. This forward-biases the synapse, because it is the relative membrane potentials (i.e. the voltage across the synapse itself, from one intracellular compartment to the other) that determines the bias state of the rectifier. Consequently, the synapse moves into a high conductance state, and negative current flows from N2 into N1, and hyperpolarizes it.

Crayfish

Rectifying electrical synapses are relatively rare, but have been found in both vertebrates and invertebrates. In fact, the very first electrophysiological demonstration of an electrical synapse was one that rectified (Furshpan and Potter, 1959). This was found in the escape tail-flip circuit of the crayfish.

Crayfish have two types of tail-flip; a backward flip when the attack is from in front, and a forward flip (actually, more of an “up-and-over” flip, but forward gives the concept …) when the attack is from the rear (see Sillar, et al., 2016 chapter 7 for review).

LG Escape. A juvenile crayfish (on the left) is attacked from the rear by a dragonfly larva. It escapes!

Video courtesy of Prof Jens Herberholz, University of Maryland.

The escapes are mediated by two giant commandCommand neuron is the name given to a single neuron that can trigger an entire behaviour when it spikes. There has been much debate about whether such neurons really exist, mainly centred around arguments about what constitutes an “entire” behaviour, but I’m going to use the term anyway. neurons, the medial giant (MG) and lateral giant (LG) respectively. TheseA fluorescent image of another large crayfish neuron, the segmental giant, is shown in the Neurosim startup screen. both cause a rapid flexion of the tail, but the shape of the flexion differs, and steers the animal in the different directions. The LG is activated by a stimulus from the rear and drives the forwards flip, while the MG is activated by a stimulus from the front, and drives the backwards flip.

In the middle part of the tail, LG and MG both make very strong electrical synapses to the same output motorneuron, another giant neuron called the motor giant (MoG). This neuron takes part in both types of tail flip. However, in other parts of the nervous system the LG and MG make outputs to different neurons, so that the overall behaviour mediated by the LG and MG is different. It is crucial to the survival of the animal that the two types don’t get mixed up!

This is a simple demonstration of the command elements of the circuit, and it shows the problem.

LG (red, top axis) is stimulated by an attack from the rear, represented by Stimulus 1. It spikes, and the spike is transmitted to the MoG (blue, middle axis) through the electrical synapse. So far, so good. However, the spike in MoG is then transmitted onwards to the MG (green, 3rd axis), which also spikes. So both the forward-specific circuit and the backward-specific circuit get activated. The same happens if there is an attack from the front activating the MG (Stimulus 2). This is not good.

To make the effect clear:

Now the two giant fibres (LG and MG) spike independently, but the MoG does not spike at all. Still not good.

The dialog box expands, and the graph on the right shows the transfer function of the synapse. The X axis is the trans-junctional potential, the Y axis is the conductance. At 0 mV (indicated by the vertical line) both neurons have identical membrane potentials, e.g. they are at rest, and the conductance is just slightly above 0. If the pre-synaptic neuron depolarizes relative to the post-synaptic neuron (e.g., it spikes), the conductance rises steeply to a maximum of 20 nS when the trans-junctional potential reaches about 30 mV. The shape of the curve is determined by a user-specified equation visible at the bottom left of the dialog box. You could use a rather simpler built-in linear equation (by selecting the Linear option from the Equation type drop-down list) if you wished.

Now the forward escape stimulus activates the LG, which goes on to activate the MoG through the forward-biased rectifying synapse, but the MoG does not go on to activate the MG, because that synapse is reverse biased. Similarly, the backward escape stimulus activates the MG and the MoG but not the LG. We no longer have cross-talk between the two escape systems. Rectification has solved the problem!

Electrical Synaptic Current

You can visualize the current through the electrical synapse as follows:

The bottom axis in the Results view shows the total current entering and/or leaving the MoG through the electrical synapses.

The current profile has a simple monophasic waveform - a pulse of positive current enters the MoG from the pre-synaptic spike in LG, and this depolarizes the Mog and induces it to spike.

The MoG current now has a tri-phasic waveform. First, a pulse of current enters the MoG (positive) from the pre-synaptic spike in LG, and as before, this is what causes the MoG to spike. Second, a pulse of current leaves the MoG (negative) as the MoG spike depolarizes the MG. Third, another pulse of current enters the MoG (positive) from the post-synaptic spike in MG. This "backwash" does not cause significant depolarization in the MoG because the latter is highly refractory at this time.

 

Dendritic Computation

An individual neuron may receive hundreds or thousands of synaptic inputs from different pre-synaptic neurons, and it is the interplay between these inputs, and the way they are integrated, that forms the basis of decision making in the nervous system. If the summed synaptic inputs take a spiking neuron above threshold, then a spike is generated and a signal passes down its axon and on to the next neuron. If threshold is not crossed, no spike occurs, and no signal is passed on. If the neuron operates with non-spiking synapses, then the summed potential is the signal, and no spikes are necessary.

Synaptic input occurs on the dendrites of neurons, and these can have very complex branching structures. Where and when an input occurs on this structure can have important consequences for signal processing.

Proximal and Distal Inhibition

The Setup view shows a highly simplified compartmental model of a vertebrate motorneuron. There is just one dendrite (the vertical line of blue blobs), which connects to the cell body (the larger purple circle at the bottom with a blue blob centre). The dendrite is non-spiking, the cell body is the spike initiating zone (SIZ) and will generate spikes if its membrane potential goes above threshold. For simplicity and speed the model does not include an axon, but if the cell body spiked, those spikes would propagate down the axon.

The compartments are coloured-coded by the membrane potential. At the moment all are at rest, hence their dark blue colour.

The distal dendritic terminal receives an excitatory synaptic input from a pre-synaptic neuron (synapse a, indicated by →). It also receives inhibitory synaptic input from another neuron (synapse b, indicated by •⸺). There is another inhibitory synaptic input from yet another neuron (synapse c, same symbol), but this occurs on the proximal dendrite, just before it enters the cell body.

The Neurosim synapse symbols have been hidden so that they don’t obscure the colours, but for clarity, show them temporarily:

We will want to edit synaptic properties during the experiments.

Stimulus 1 activates the excitatory pre-synaptic neuron (green trace in the top axis in the Results view: Distal E) which puts EPSPs onto the distal dendrite (blue trace in the 4th axis in the Results view: Distal post). The synapse is quite powerful, and the distal post-synaptic membrane potential approaches the equilibrium potential of the synapse at -10 mV. This depolarization spreads down the dendrite by passive conduction, and although it attenuates, it is still above threshold when it reaches the SIZ, which consequently spikes (blue trace in the bottom axis: SIZ).

The distal inhibition partially counteracts the distal excitation thus producing smaller EPSPs in the distal dentrite (4th axis), and the membrane potential at the SIZ (bottom axis) no longer reaches threshold. Hopefully, this all makes sense.

Now the SIZ spikes again.

We could now prevent spiking by increasing the strength of the inhibition (type b: IPSP (distal), and then restore it by further increasing the strength of the type a excitation. Basically, the two synapses are in competition with each other, and the strongest wins.

The proximal inhibition completely obliterates the excitation at the SIZ, even though it has much lower synaptic strength. Furthermore, increasing the strength of the distal excitation cannot overcome this proximal inhibition.

Despite the huge increase in excitation, there is virtually no increase in the membrane potential at the SIZ, and the inhibition is highly effective.

Question: Why cannot the proximal inhibition be overcome by increasing distal excitation?

I’m going to try to explain this (based on Vu and Krasne, 1992), so if you are stuck on the question, just read on.

When an EPSP occurs on the distal dendrite, intracellular current flows from the distal to the proximal region because the distal membrane is depolarized relative to the proximal membrane. The greater that depolarization, the more current flows (Ohm's Law) and the greater the excitatory effect. However, there is a ceiling to the voltage that the distal dendrite can ever reach, and that is the equilibrium potential of the excitatory synapse (-10 mV in this case). So a massive increase in distal excitatory synaptic conductance “locks” the distal dendrite firmly to that voltage, but can never take it beyond it – it cannot make it still more positive. Distal inhibition will tend to drag the distal membrane potential negative from this equilibrium potential, so increasing excitatory conductance can pull it back up again and restore excitation – the two can compete with each other.

Proximal inhibition does not work by pulling the distal membrane potential negative. It simply tries to lock the membrane potential at the SIZ to the inhibitory equilibrium potential. Since the excitatory synapse cannot increase the distal voltage above its own equilibrium potential, it cannot drive more positive current proximally to overcome the proximal inhibition, no matter how strong it is.

So it is likely that evolution tunes the location and activation of inhibition according to its function. If responding to an excitatory stimulus would be seriously inappropriate (e.g. fatal) in a particular situation, that situation should activate proximal inhibition, with the excitation being delivered distally. The inhibition can then override the excitation, no matter how strong the latter is. But if the inhibition and excitation should compete on more-or-less equal terms, then they should be co-located in the same distal dendritic region, so that the outcome just depends on which is the stronger.

Take-home message. Distal inhibition can be overcome by increasing distal excitation, but proximal inhibition can be absolute – if it is above a certain strength, it cannot be overcome by increasing distal excitation.

Directional Sensitivity

The Setup view shows two almost identical small circuits labelled Circuit 1 and Circuit 2.

Within each circuit, on the left is a simplified compartmental model of a sensory interneuron. As in the previous simulation, there is just one dendrite (the vertical line of blue blobs), which connects to the cell body (the purple circle with a blue blob centre). The dendrite is non-spiking, the cell body is the spike initiating zone (SIZ) and will generate spikes if its membrane potential goes above threshold. For simplicity and speed the model does not include an axon, but if the cell body spiked, those spikes would propagate down the axon.

On the right within the circuit is an array of sensory neurons which make mapped input onto the dendrite. These are supposed to have contiguous receptive fields in real space.

Each sensory neuron within a circuit is activated in turn by a stimulus, and the two circuits get activated simultaneously. The only difference between the two circuits is the order in which the sensory neurons get activated.

The stimuli have been arranged so that each sensory neuron is activated in top-to-bottom temporal sequence (you can see their colour change as they are activated). This is the equivalent to a sensory stimulus sweeping across the receptive field from top to bottom. The dendrite thus receives excitatory synaptic input in a distal-to-proximal temporal sequence.

In the Results view, the top axis shows the sensory neuron responses in circuit 1 superimposed. The second axis shows the interneuron membrane potential at the SIZ (the red trace). The EPSPs impinging on the dendrite passively conduct to the SIZ, where they summate sufficiently to cause a spike.

In circuit 2 the colour change sweeps from bottom to top, which is as though the sensory stimulus swept across the receptive field in the opposite direction (i.e. proximal-to-distal). In the Results view it is apparent that the sensory neurons in the third axis are activated in the opposite sequence (the traces are colour coded in shades of blue). There is less summation at the SIZ (red trace), and the SIZ does not spike.

We all know from subjective experience that we can detect the difference between seeing something moving downwards in our field of view, and the same object moving upwards. What this simulation shows is that the difference can be detected even at the level of a single neuron (although of course there is a lot more than that going on in our brains).

Take-home message: Synaptic integration can depend both on the spatial arrangement of synaptic inputs on the dendritic tree, and on the temporal sequence in which they are activated.

 

On to Networks ...