CONTENTS Passive Properties
Nernst equation: Equilibrium and reversal potential Goldman equation: Goldman-Hodgkin-Katz constant field equation Pumps: Na/K exchange pump Permeability vs Conductance
Basic RC properties Input resistance Membrane time constant Low-pass filter
Attenuation and delay: Basic cable properties Space (length) constant: : Attenuation with distance Time constant: Time delay with distance Input resistance Non-uniform diameter: A compartmental model Spatial summation
Units: Passive property units Action Potentials (Spikes) Spike Conceptual Summary
Threshold: All-or-none? Sodium Dependence Hyperkalaemia: Too much extracellular potassium Spike Currents and Conductance Molecular Events: Single-channel patch recording Strength-Duration Curve Refractory Period Threshold Accommodation Rebound Excitation: Post-inhibitory rebound Pacemaker: Continuous regular spiking
Basic Conduction Features Collision Spatial Distribution: Voltage profile along the axon Passive vs Active Conduction: A qualitative comparison Refractory Conduction Myelination and Saltatory Conduction
Theory Classic HH: How to get a Nobel prize Sodium IV Curve Potassium IV Curve Capacitive Current: Importance in voltage clamp mechanism Patch Recording: Single channel recording under voltage clamp
Endogenous Bursters Plateau Potentials A Current: Fast (transient) potassium current
Gate Voltage Dependency Channel Voltage Dependency Putting it Together: Finding the membrane potential Non-Ohmic Channels: The GHK current equation Reduced Models: Morris-Lecar and others Phase Plane Analysis
Synapses
Excitation and Inhibition Voltage Clamp: Applied to synaptic potentials Summation and Facilitation Depolarizing and Silent IPSPs Non-Spiking Synapses Voltage-Dependent Synapses: NMDA-type Hebbian Synapses: The basis of memory? Quantal Release
Frequency Matters Size Matters Rectification
Proximal and Distal Inhibtion Directional Sensitivity
Networks
Flip-Flop Circuit Reciprocal Inhibition Oscillator Multi Phase Rhythms Sensory Feedback Phase Resetting Tests Tadpole Swimming: A case study Synchronization and Entrainment
Stochastic Resonance: Noise matters Lateral Inhibition
Primary Afferent Depolarization (PAD)
Phase Ambiguity
Classical Conditioning: Pavlov's dog Associative Learning: Pattern completion Facilities for Memory Models
Theory: Population-level coding in the Wilson-Cowan model Neurosim Implementation Stable States Oscillations Multi-Unit Models
Single-Channel Kinetics
Sojourn Duration and Transition Rate Constants Sojourn Distribution is Exponential
Open-Time Distribution Closed-Time Distribution is Multi-Exponential
What's the Point?: A reminder
Open-Time Distribution Closed-Time Distribution
Acetylcholine Receptor Model Auto-Correlation Compartmental Models Active Currents Neurosim Implementation Implementation
Passive Properties Noise Spiking Properties Voltage-Dependent Channels Ca-Dependent Channels Sodium Pump
Spiking Chemical Synapses Non-Spiking Chemical Synapses Carrier Ions: Calcium and sodium Electrical Synapses
Exponential Euler Integration Integration Components Adaptive Step Size Wilson-Cowan integration
References
Contents

Copyright © W. J. Heitler (2019)

Compartmental Models

A small patch of membrane or a simple spherical cell can be modelled as an isopotential RC (resistor-capacitor) circuit. Dendrites or axons which are long and have uniform properties are not isopotential, but they can be modelled using the cable equation. However, once you start dealing with more complex anatomical structures such as branching dendrites, and dendrites that change in diameter, there are no simple algorithmic solutions that tell us what happens to the membrane potential in one region of the cell, when there are voltage and/or current changes in another region. To find that out you must build a compartmental model.

The concept behind compartmental modelling is very simple. You just break a complex structure up into a series of small compartments (e.g. cylindrical sections of a dendrite), each of which can be treated as an isopotential RC circuit. You then connect the interior face of the RC circuit of one compartment to the interior faces of the circuits of adjacent compartments, using a conductor to represent the intracellular electrolyte. The extracellular face of all compartments is held at ground potential, on the basis that extracellular resistance is normally very low.

If there is a voltage difference between adjacent compartments, current will flow out of one compartment and into the other, acting as a negative and positive stimulus current respectively.

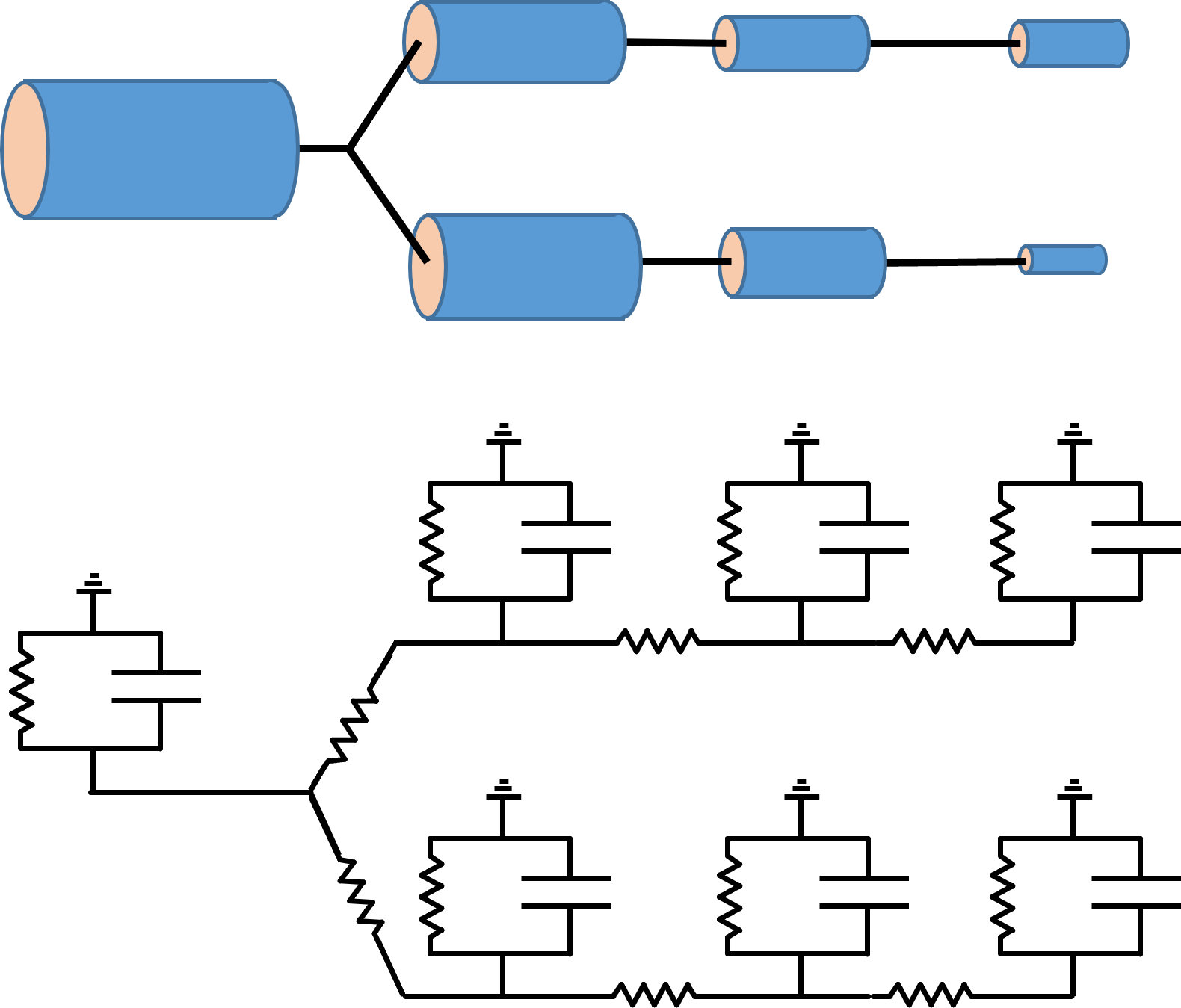
Comparmental model
Compartmental model. A complex structure is broken up into small, uniform, connected compartments.

If you make the compartments small enough, and if you can accurately specify the membrane conductance and capacitance for each compartment, and the intracellular coupling between compartments, then the circuit can provide an accurate description of the passive distribution of voltage within the structure. However, there are a lot of ifs there – usually you have to make inspired guesses for at least some of these parameters.

Active currents

The circuit shown above only contains resistors and capacitors – it is a purely passive circuit. It can be made more realistic, and more complex, by adding voltage-dependent or synaptic channels to appropriate compartments. So compartments representing sections of dendrites might have synaptic channels but no voltage-dependent channels, compartments representing the axon might have voltage-dependent channels but no synaptic channels, and the cell body compartment might have both synaptic and voltage-dependent channels.

Each channel is represented in the compartment by adding a variable resistor in series with a battery. The battery has the EMF of the equilibrium potential of the ion that passes through the channel, and the resistance of the channel varies according to its controlling factor – voltage or ligand binding etc. (for the leakage conductance, the resistance is fixed).

Describing the behaviour of such a circuit requires solving multiple differential equations simultaneously, which can only be achieved by iterative numerical integration. It rapidly becomes very computationally demanding as the number of compartments increases. However, the real problem is not computing power, it's the number of interacting parameters that have to be specified. It is very difficult to acquire experimental evidence to justify all the numerical values that need to be provided, and guesswork can rapidly lead the modeller down the rabbit hole known as "the curse of dimensionality", resulting in him or her becoming "lost in parameter space". An informative (and quite entertaining) review of this problem is provided by Almog and Korngreen (2016).

Neurosim Implementation

SimpleNeurosim is not intended to be a fully-featured compartmental modelling solution. For such an activity I recommend specialist programs such as Genesis or Neuron compartmental models can be built using the Network module in Neurosim, by linking together chains of individual neurons with electrical synapses. If these synapses are given a very high conductance they become the equivalent of simple cytoplasmic continuity, and then the circuit becomes a compartmental model in which the neurons are the compartments.

Compartmental coupling. In Neurosim, coupling between compartments is implemented as electrical synapses (the zig-zag resistor symbols) between cells.

In the Network module, neurons are treated as spherical structures with a specified diameter, and have membrane properties (conductance, capacitance etc.) specified per unit area. To turn them into compartments with equivalent electrical characteristics, they need to be treated as open-ended cylinders with the same surface area. This is simple because a sphere with diameter d has the same surface area as an open-ended cylinder of diameter d and length d. However, this does mean that in Neurosim you cannot independently specify the diameter and length of a compartment, the two go together. This means there might be a trade-off between accuracy and efficiency: in general the shorter the length of a compartment the higher the accuracy of the model, but you may end up with more compartments than are needed for the structure.

In Neurosim, electrical synapses are specified with an absolute conductance value. However, to maintain a constant cytoplasmic resistivity, the electrical synaptic conductance representing the cytoplasm needs to be scaled with compartment diameter. The scaling factor is simple proportionalityDoubling the diameter of a compartment increases the intracellular conductance by a factor of 4 (2 squared) due to cylinder cross-section area considerations, but also halves it due to the cylinder length doubling, leading to a linear proportionality.: if you double the compartment diameter, you need to double the conductance of the electrical synapse linking them.  You do this by specifying different sub-types of electrical synapse between compartments that differ in size. But note that there is a limit of 26 different sub-types of synapse, so there is a maximum of 26 different compartment sizes (although you can have many more compartments in total, if you wish).