Walk-Through: Build a Neuron

Neurosim can replicate many published neuronal models, particularly those based on a single-compartment HH-type formalism. As an example, we will build a neuron from the description given by Butera, et al., 1999. This simulates a neuron from the region of the mammalian brain that is involved in generating the respiratory rhythm. The neuron has interesting properties because it can be silent, or show a steady spike frequency (pacemaker activity), or show rhythmic bursts of spikes, depending on the level of stimulation.

Start Neurosim and activate the Advanced HH module.
Select the first synapse in the Synapses box (A: Nicotinic ACh) by clicking it, and uncheck the Active box to switch it off.
Select the Channels: Delete all menu command.

We have now got a neuron with a purely passive membrane that we can build on. It may be a good idea to save this, and to continue to save (with a new name each time) repeatedly as you build the model, so that you can retrieve an earlier version if something goes wrong.

Select the menu command File: Save As and give the file an appropriate name, e.g. Butera 1

A read-through of the paper shows that the neuron has 3 voltage-dependent channels plus the usual leakage channel. The voltage-dependent channel kinetics are specified in terms of the time-infinity open probability and time constant of the activation and inactivation gates that they contain. Since the kinetic equations do not exactly match the build-in types in Neurosim, we will specify user-defined equations for the kinetics, when we come to them.

One immediate problem is that the Butera paper gives the channel conductances and membrane capacitance as absolute values, but Neurosim expects this type of parameter as an area-specific value, i.e. per square centimetre, so some conversion will be needed.

Here is a list of the parameters that we need to covert, and their target absolute values. The right-hand column in red has been pre-filled with calculated values obtained as described below the table.

Parameter	Target Absolute value	Calculated Area-Specific value (diameter = 25.85 µm)
Membrane capacitance	21 pF	1
Leak conductance	2.8 nS	0.1333 mS/cm²
Fast sodium maximum conductance	28 nS	1.333 mS/cm²
Persistent sodium maximum conductance	2.8 nS	0.1333 mS/cm²
Potassium maximum conductance	11.2 nS	0.5335 mS/cm²

To convert to area-specific values we need to know the area, but the paper does not specify the neuron’s size. However, if we assume an area-specific capacitance of 1 µF/cm², which is a typical value for phospholipid membrane, we can calculate the surface area and hence cell diameter (assuming the cell is spherical) from the absolute capacitance, and then scale the conductance values appropriately.

You could now sit down with a calculator or Excel and write some formulae to do the maths, but alternatively you can get Neurosim to do the work:

Surface Scaling Helper

Select the Options: Surface scaling helper menu command to open the Spherical Surface Scaling Helper dialog.
If possible, move the dialog so that it does not obscure the main program.

Note: the surface scaling helper is new in version 5-5. If you are running an earlier version, then follow the tutorial here.

This is a non-modal utility dialog designed to help make the sort of conversions that we need here. Note that the dialog is also available from the Options menu in the Network module.

The first task is to calculate the size (diameter) of the neuron.

Select Absolute capacitance from the Diameter value source options group (at the top-right of the dialog).

This tells the dialog that we want to derive the diameter from the absolute capacitance. It sets the area-specific capacitance value to 1 µF/cm² (because that is the generally-accepted "best-guess" value) and disables its edit box.

Enter 21 into the Capacitance box in the Absolute value column (near the bottom-left of the dialog).
Press the TAB key to accept the edit.

The Diameter box (at the top-left of the dialog) now shows a value of 25.85 µm. Note this down (or directly edit the neuron diameter, as described later).

Next we want to calculate the area-specific conductance values for the various channels using this new diameter. The paper specifies the absolute leak conductance as 2.8 nS.

Enter 2.8 into the box in the Conductance row, Absolute value column.

The value in the Unit area column changes to 0.1333+ mS/cm². This is the required area-specific leak conductance for this size of neuron, given the absolute leak conductance value. Note the value.

In turn, enter the absolute conductance values for each channel (as listed in the Target Absolute value column of the table above) and note the various area-specific conductances.

You should end up with the values that are shown in red in the right-hand column of the table.

The Scaling Helper dialog also allows conversion in the other direction. If you edit a value in the Unit area column, then the Absolute value changes appropriately. The dialog can also calculate spherical diameter from surface area or volume, and vice versa.

Passive Properties

The neuron is represented in the Setup view by the green circle in the blue-ish preparation bath, and its diameter is shown in the middle. The diameter is currently at its default value of 50 µm.

Enter the new diameter value 25.8544 into this edit box.
You could copy-and-paste this from the Scaling Helper dialog.
Check the Passive box in the Cell properties group (to the right of the bath) to open the Passive Properties dialog.
Enter 0.1333 into the area-specific Leak conductance box (top row).
Note that the absolute leak conductance changes to 2.7993 nS, which is close enough to the target value of 2.8 nS.
Set the leak equilibrium potential to -65 mV.
Click OK in the Passive Properties dialog to confirm the entries and dismiss the dialog. (Clicking Apply confirms the entries but leaves the dialog open.)

It’s probably sensible to save again (Butera 2) before starting on the voltage-dependent channels. You could also click Start just to make sure things are still working.

Voltage-Dependent Channels

For reasons that will become apparent, the first channel we will add is the delayed rectifier potassium channel.

Delayed Rectifier Potassium Channel

Select the menu command Channels: Add

This adds a voltage-dependent channel to the neuron, with its starting values set to those of the HH sodium channel in the squid. The Voltage-Dependent Channel Properties dialog opens automatically to show the parameter values for the new channel. We now need to edit those value.

Set the channel Description as “K delayed rectifier”.
Set the Short name as “Kdr”
Set the Trace colour to blue (or any other colour of your choice)
- Click on the Trace colour button (the coloured block beside the label Trace colour), and select the desired colour from the Colors dialog.
Set the Equilibrium potential to -85 mV.
Set the Maximum conductance to 0.5335 mS/cm² (the value obtained earlier from the absolute conductance of 11.2 given in the Butera paper).

Kinetics

The potassium channel has 4 activation gates and no inactivation gate, so we need to adjust the gates:

Select the second gate in the list [Na: h (inactivation)] by clicking it.
Click the Del button to remove the gate.
Set the Description of the remaining gate to just n.
We need to change the exponent, but we cannot do that yet because the gate is still specified as an exact HH gate with a fixed exponent.
Uncheck all the OK boxes in the Equations group.
In the Equations group, select the User-defined: inf/tau (∞, τ) equation option (i.e. the top-right radio choice button).
Now set the gate number Exp # to 4, before we forget.
Set the Inf var equation to 1 / (1 + exp((v - -29) / -4)). (You can just copy and paste the bold text here and below.)
Set the Time const equation to 10 / cosh((v - -29) / (2 * -4)).

[Hint: If you are starting from scratch, it is easier to write equations externally in a plain-text editor like Notepad, and then copy and paste them into Neurosim. If you edit them directly and make a syntax mistake like not closing a bracket, the parser warns you, but then replaces your text with the previous text. This can be frustrating if you typed in a lot of complex text. Also, the equation parser is fast, and pre-calculates known values, so there is not much to be gained by hand-optimizing expressions.]

Check the OK box beside the equation choice to indicate that the parameters are valid. (This is not essential, it's just a visual reminder.)
Click the Apply button at the bottom of the Channel Properties dialog.

At this stage a reality check may be in order:

Check the Show graph box at the bottom right of the Equations group.

The Channel dialog will expand to show the K channel kinetics.

The default display should show the sigmoid curve of the steady-state open probability. It has the right shape (increasing open probability with depolarization) and, if you hover the mouse over the midpoint, you will see that the X value is about -30 mV. This is both reasonable for a voltage-dependent channel activation curve, and fits with the equation, which shows that the actual mid-point is -29 mV.
Select the Time constant option in the Display group above the kinetic graph. Note that the maximum time constant is 10 ms, which seems reasonable for a potassium channel, and the membrane potential at the maximum is -29 mV, which again fits with the equation.

The Voltage-Dependent Channel Properties dialog should now look like this:

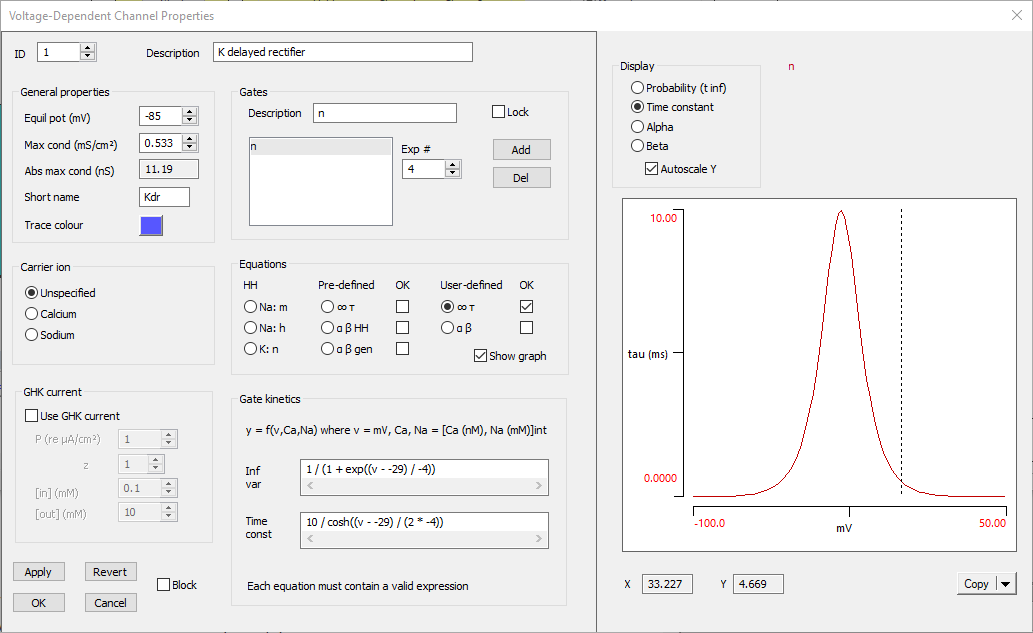
Voltage-dependent channel properties dialog

The voltage-dependent potassium channel is now complete. It is probably a good idea to save the file again (Butera 3).

Fast Sodium Channel

Now we will add the main sodium channel that makes spikes.

Select the menu command Channels: Add

A new channel is made with ID 2, and again it has the properties of an exact HH sodium channel. Some of these are OK, but others need to be edited. Assuming that the Voltage-Dependent Channel Properties dialog box is still open:

Set the channel Description as “Na fast”.
Set the Short name to “Naf”
Leave the Trace colour as red.
Set the Equilibrium potential to 50 mV.
Set the Maximum conductance to 1.333 mS/cm² to get an absolute maximum conductance of about 28 nS.

Kinetics

For consistency, rename the two gate types as m and h.
As for the potassium channel, set both gate type equations to User-defined: inf/tau and adjust the validation OK marks.
The exponent values of 3 for m and 1 for h are correct, so leave these unchanged
Select the m gate by clicking it in the list.
Set the Inf var equation to 1 / (1 + exp((v - -34) / -5)).
Set the Time const equation to 0.
The paper specifies that m gates are effectively instantaneous, so a time constant of zero is appropriate.
Select the h gate by clicking it in the list.

The paper specifies that h = 1 – n. We cannot explicitly specify this internally in Neurosim, so we set an h gate whose equation mirrors those for the n gate. This is computationally less efficient (we calculate the same equation twice), but that is the penalty of a generalizable program.

Set the Inf var equation to 1 - 1 / (1 + exp((v - -29) / -4))
(i.e. 1 – n_∞).
Set the Time const equation to exactly that of the K channel, i.e. 10 / cosh((v - -29) / (2 * -4)).
In the graph section of the dialog, select Probability (t inf) in the display group.

Note that now there are two lines - the upward sloping line for the m activation variable, and the downward sloping line for the h inactivation variable.

Click Apply to accept the entries.
Now switch between channel ID 1 and 2 (in the top-left of the dialog).

You can see that the potassium channel (1) only has an activation curve, and that it activates at a slightly higher membrane potential than the sodium channel (2). Again, this fits with the equations.

Click OK to accept the entries and dismiss the Properties dialog box.

Save the file again (Butera 4). At this stage it is probably a good idea to do a reality check on the Na and K channels.

Select Voltage in the Clamp mode group in the Stimulating section of the Setup view.
Click the Traces button in the Results view.

Change the entries in the current and conductance traces from A (the now-inactive synapse) to 1 2 (our new K and Na channels).
Click OK.

Click Start.
Hold down the control key and click the Autoscale button () in the Results toolbar.

The current and conductance traces should look very much like those in a standard HH-type voltage clamp experiment. HOWEVER, there is something a bit different about the sodium inactivation. Inactivation certainly occurs – the sodium conductance (bottom trace, red) increases then auto-terminates in each clamp step, as it should. However, the second clamp step produces a peak sodium conductance which is virtually identical to the first. There is little sign of persistent inactivation.

Clear the screen, reduce the clamp interval to 0.1 ms in the Setup view, and Start another experiment.

Now there is evidence for persistent sodium inactivation. Evidently de-inactivation occurs really quickly in this neuron. Why is this?

Double-click Na fast in the channel list to show its properties again.
Click h in the gate list to select it.
Check the Show graph box under the Equations choices.
Select Time constant from the Display options.

The h time constant follows a bell-shaped curve with a peak at 10 ms, but the centre is at about -30 mV. At the voltage-clamp holding potential range of -70 mV the time constant is only about 0.5 ms. This is why the sodium channel recovers from inactivation so quickly when the neuron repolarizes.

Persistent Sodium Channel

The final channel to add is the persistent sodium channel. The channel has this name because it inactivates very slowly. We could simply Add a channel as we did previously, but we can also base the new channel on the existing sodium channel.

Click 2: Na fast in the Channels list in the Setup view to select it.
Select the menu command Channels: Copy. This places a copy of the channel onto the clipboard, but the format is Neurosim-specific so the channel cannot be pasted into another program (but it could be pasted into another instance of Neurosim, or into a neuron in the Network module.
Select the menu command Channels: Paste.

A new channel is made with ID 3 and the channel properties dialog opens automatically, with this channel selected. At the moment it is an exact copy of the existing Na fast channel.

Set the channel Description as “Na persistent”.
Set the Short name as “Nap”
Set the Trace colour to green (or any other contrasting colour).
Keep the Equilibrium potential at 50 mV (unchanged from the fast Na channel).
Set the Maximum conductance to 0.133 mS/cm² (from table above). Note that this is one tenth of the fast sodium channel
Select the m gate by clicking it in the list.
Set the Exp # to 1.
Set the Inf var equation to 1 / (1 + exp((v - -40) / -6)).
Set the Time const equation to 0.
Select the h gate by clicking it in the list.
Set the Inf var equation to 1 / (1 + exp((v - -48) / 6)).
Set the Time const equation to 10000 / cosh((v - -48) / (2 * 6)).
Note the very long numerator value. This makes inactivation a slow process in this channel.

At this point it is worth doing another reality check.

Click Apply to “lock in” the new persistent sodium channel.
Check the Show graph box below the equation type choices.

The dialog expands to show the voltage-dependency of the various gate parameters. The default view shows the open Probability of the gates; check that activation gate probabilities increase with depolarization (slope up to the right), and inactivation (if any) probabilities decrease (slope down to the right). You can check the time constants by selecting the Time constant display option. The time constants should all have a bell curve (or be zero), but their peak values and the location of the peaks vary.

Look at the open probability and time constant of each channel type in turn (change the ID value at the top left to change the channel).
If you are happy that it all makes sense, click OK to dismiss the dialog.
You should definitely save the file (Butera 5)!

Now is a good time to test the model and see how it behaves

Set the stimulus mode to Current clamp.
Click the Traces button in the Results view.

Change the entries in the current and conductance traces from A (the now-inactive synapse) to 1 2 3 (our new K and Na channels).
Click OK.

Click Start.
Hold down the control key and click the Autoscale button () in the Results toolbar.

Your Results view should now show this:

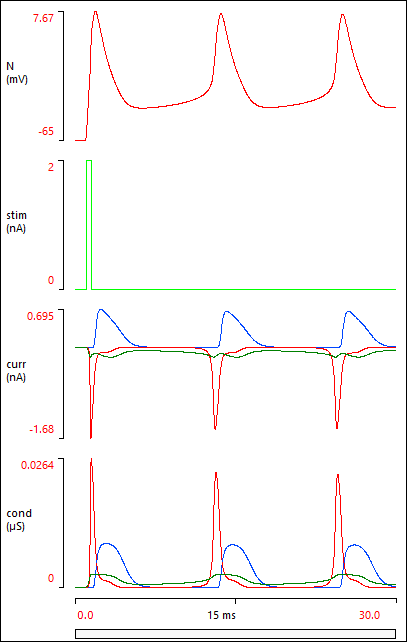
Final Butera model

If your Results do not look like the image above, it probably means that you have made a data entry error somewhere. You can load a pre-built parameter file Butera final, and check this against your own model. Note that the Options: Configure view menu command has been used to remove some unused elements from the Setup view.

Exploring the Model

The Results above show that a brief depolarizing stimulus elicits a spike, but clearly there are some more spikes that follow on.

Clear the screen and set the right-hand time base scale to 1000 ms.
Click Start again.

The stimulus elicits a burst of spikes, but this terminates after about half a second. This is an example of a plateau potential - a depolarizing response which outlasts the stimulus that initiates it.

Here are some stimulus regimes that produce a variety of results:

Load and Start the file Butera bursts.

Note that Scroll has been selected as the Trigger mode in the Results view.

As the filename implies, the neuron produces regular bursts of spikes. This is exactly the same neuron, but a tonic stimulus is applied to depolarize the neuron (Pulse 1, Amplitude 0.016, Duration huge!). The initial resting potential (in the passive properties) has been set to -50 mV, so that the simulation stabilizes to its depolarized state more quickly. Also, note that the timebase is set to display in seconds rather than milliseconds (using the View: Time units menu command).

The top trace is the membrane potential, the middle trace is the stimulus, and the bottom trace is the activation and inactivation gate open probabilities of the persistent sodium channel. The oscillations are primarily driven by oscillations in this channel.

Click Clear.
Select the K delayed rectifier channel in the channel list (the first channel).
Check the Block box above the list. Note that the channel name now has “[blocked]” in front of it.
Do the same to block the Na fast channel.
Click Start.

The membrane potential still oscillates! The activation and inactivation of the persistent sodium channel can be seen more clearly now that the neuron no longer generates fast HH-type spikes.

Unblock the fast channels by reversing the procedure above.
Increase the stimulus amplitude to 0.02 nA.
Click Start.

Note that the oscillations are now considerably faster. There is an extra large burst at the beginning before the system stabilizes into a steady state, but this could be avoided by setting a slightly depolarized initial resting potential of -48 mV.

Increase the stimulus amplitude again, this time to 0.025 nA.
Click Start.

After a few seconds of simulation time to achieve a steady state, the neuron produces a steady constant-frequency train of spikes. This is known as pacemaker activity.
You can observe the gamut of activity with a ramp stimulus.

Set the Ramp of Pulse 1 to 50000 ms (50 s).
Click Start.

The neuron goes from silent, to bursting, to pacemaker activity, as the stimulus strength gradually increases.

When the simulation run completes (after 60 s), click the Show all button () on the Results toolbar.

You should now see something like this:

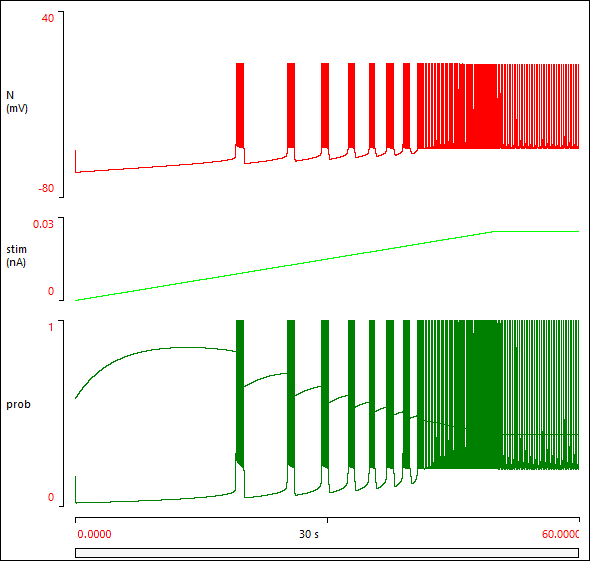
Butera ramp stimulus

Incorporating the Neuron into a Network

Neurons which have been designed and built in the Advanced HH module can be incorporated into circuits in the Network module if desired.

Use the Neuron: Save menu command to save the neuron with a suitable name, e.g. Butera. The file extension "nrsm-nrn" will be automatically applied.
Switch to the Network module using the Model: Network command.

We can either use the Neuron: Load menu command to load a new neuron and place it in the circuit, or we can take an existing neuron and modify its properties. We will do the latter, but starting from a minimum circuit.

Select the Neuron: Delete all menu command to make a circuit with just one neuron.
Double-click the neuron (the yellow circle in the Setup view) to open the Neuron Properties dialog.
Click the Load properties button in the top-right corner of the dialog.
Choose the neuron that you have just built and saved in the Advanced HH module.

Note that the neuron now has the diameter and passive properties as previously specified, and the three voltage-dependent channels show in the channel list.

To replicate the bursting activity of the previous simulation, we can add some tonic current.

Check the Tonic input box near the top-right of the dialog.
Set the Constant current stimulus to 0.0167 nA.
Click OK in the Neuron Properties dialog. This will shut down both the Properties and the Tonic input dialogs, and “lock in” the changes.
In the Results view, set the right-hand time base to 8 s (note that the units are in seconds, not milliseconds).
Click Start.

There are two problems with the Results display. The first is that we have left-over traces from the default start-up condition. The second is that output from our neuron looks rather "ragged", with varying spike heights and burst durations. The former is easily fixed:

Clear the screen.
Click the Traces button.
- Uncheck the Show boxes for axes 2 and 3 in the Trace and Axis Setup dialog.
- Click OK to dismiss the dialog.

The second problem is caused by the integration step still being at the default value for integrate-and-fire neurons in Network module. This is too big for a full HH model.

Select the Options: Integration menu command to open the Integration dialog.
- Set the integration time step to 0.05 ms.
- Click OK.
Click Start to run the simulation again.

The Results display looks better. Choosing the integration time step in Neurosim is largely a matter of trial-and-error. If you suspect the step is too large, you can make successive reductions until there is not much change in the display - at that point you have probably achieved a satisfactory value.

There is also a cosmetic problem with the Setup view - the yellow circle representing the neuron is rather small. This reflects the reduced diameter of the neuron, but since there are no other neurons for comparison, it would be nice if it were bigger.

Select the Options: Configure view menu command to open the Configure View dialog.
- Set the Default neuron radius to 18.
- Click OK to close the dialog.

This has not changed the physiology at all - the neuron's functional diameter is still 25.85 µm, it is just drawn as a bigger circle in the view.

Mix Integrate-and-Fire and HH

The neuron currently uses the persistent Na channel to generate the oscillations, and HH-type Na and K channels to generate spikes. We could replace the latter with the integrate-and-fire mechanism. This should be faster to compute, which might be important if we were building a network with a lot of neurons.

We will generate another neuron, and replace the Butera HH-type spike mechanism with the integrate-and-fire process.

Hold down the control key on the keyboard, and click and drag the neuron in the Setup view to a new location. This will duplicate the original neuron, so that you now have two identical neurons, each with the Butera burst mechanism.
Click the Traces button to open the Trace and Axis Setup dialog again.
- Check the Show box for axis 2.
- Enter 2 in the Neurons column for axis 2. This means that neuron 2 will display on axis 2, while the original neuron 1 continues to display on axis 1.
- Click OK.
Click Start to check that both neurons are displaying properly. At this point their displays should be identical.
Double-click neuron 2 to open the Neuron Properties dialog again.
Click the K delayed rectifier channel in the Voltage-dependent channels list to select it.
Click the Del button to delete that channel.
Repeat for the Na fast channel.
Click Start to make sure things are OK.

You should see a single non-spiking oscillation (without the voltage-dependent spikes, the rhythm slows down somewhat due to reduced activation of the persistent sodium channel).

Check the Use integrate-and-fire spikes box in the Neuron Properties dialog.
Click Start.

You should now see tonic spikes occurring, which is not quite what we expected. However, the integrate-and-fire mechanism does have a voltage-dependent after-hyperpolarization, and maybe this is pushing the neuron into pacemaker (tonic firing) mode.

Reduce the AHP conductance to 0.2 mS/cm².
Clear the screen and click Start.
Click OK to dismiss the Neuron properties dialog, accepting all the changes.

Now we have a burst of spikes which is about the same duration as the underlying oscillation. The dynamics of the oscillations and spikes are not the same, but this is not surprising given the difference in the generation mechanisms. There are several facilities within the integrate-and-fire properties that can be adjusted to modify spike frequency.

The parameter file butera network is supplied in case you want to check your own working.

NEXT