Copyright © W. J. Heitler (2019)
Compartmental Models
A small patch of membrane or a simple spherical cell can be modelled as an isopotential RC (resistor-capacitor) circuit. Dendrites or axons which are long and have uniform properties are not isopotential, but their passive properties can be modelled using the cable equation. However, once you start dealing with more complex anatomical structures such as branching dendrites, and dendrites that change in diameter, there are no simple algorithmic solutions that tell us what happens to the membrane potential in one region of the cell, when there are voltage and/or current changes in another region. To find that out you must build a compartmental model.
The concept behind compartmental modelling is very simple. You just break a complex structure up into a series of small compartments (e.g. cylindrical sections of a dendrite), each of which can be treated as an isopotential RC circuit. You then connect the interior face of the RC circuit of one compartment to the interior faces of the circuits of adjacent compartments, using a conductor to represent the intracellular electrolyte. The extracellular face of all compartments is held at ground potential, on the basis that extracellular resistance is normally very low.
If there is a voltage difference between adjacent compartments, current will flow out of one compartment and into the other, acting as a negative and positive stimulus current respectivelyEssentially, this is functionally the same as independent single-compartment neurons coupled by powerful electrical synapses..
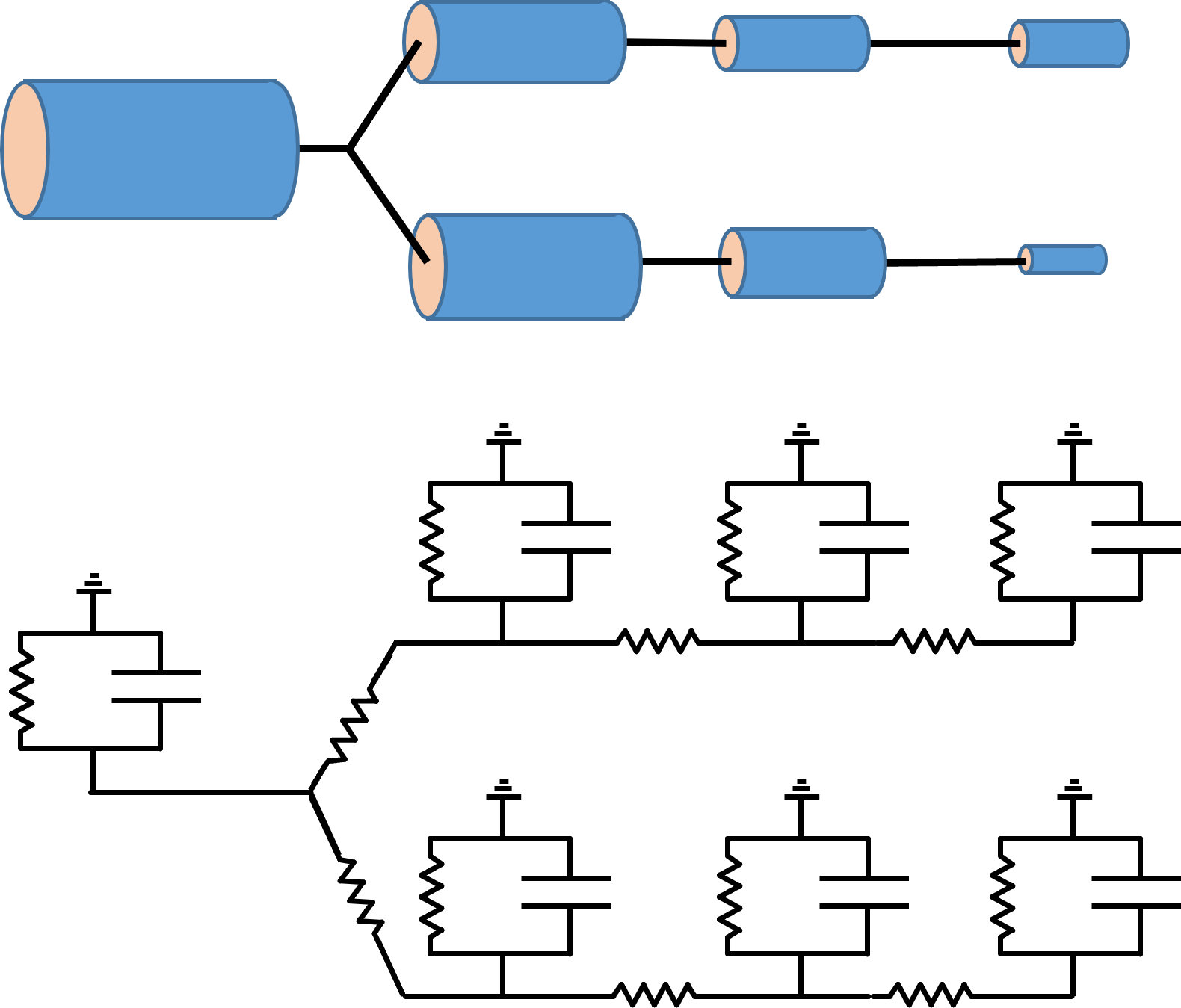
If you make the compartments small enough, and if you can accurately specify the membrane conductance and capacitance for each compartment, and the intracellular coupling between compartments, then the circuit can provide an accurate description of the passive distribution of voltage within the structure. However, there are a lot of ifs there – usually you have to make inspired guesses for at least some of these parameters.
Active currents
The circuit shown above only contains resistors and capacitors – it is a purely passive circuit. It can be made more realistic, and more complex, by adding voltage-dependent or synaptic channels to appropriate compartments. So compartments representing sections of dendrites might have synaptic channels but no voltage-dependent channels, compartments representing the axon might have voltage-dependent channels but no synaptic channels, and the cell body compartment might have both synaptic and voltage-dependent channels.
Each channel is represented in the compartment by adding a variable resistor in series with a battery. The battery has the EMF of the equilibrium potential of the ion that passes through the channel, and the resistance of the channel varies according to its controlling factor – voltage or ligand binding etc. (for the leakage conductance, the resistance is fixed).
Describing the behaviour of such a circuit requires solving multiple differential equations simultaneously, which can only be achieved by iterative numerical integration. It rapidly becomes very computationally demanding as the number of compartments increases. However, the real problem is not computing power, it's the number of interacting parameters that have to be specified. It is very difficult to acquire experimental evidence to justify all the numerical values that need to be provided, and guesswork can rapidly lead the modeller down the rabbit hole known as "the curse of dimensionality", resulting in him or her becoming "lost in parameter space". An informative (and quite entertaining) review of this problem is provided by Almog and Korngreen (2016).
Neurosim Implementation
Compartmental models can be built using the Network module in Neurosim, by linking together chains of individual neurons with internal coupling resistances. These resistances (reciprocal conductances) effectively mediate cytoplasmic continuity, and then the circuit becomes a compartmental model in which the neurons are the compartments.
A compartment can be designated to have spherical or cylindrical shape. The former is suitable for the cell body, the latter for dendrite or axonal compartments (but see Limitations below).
Cytoplasm is assumed to have a single user-specified resistivity which is shared by all compartments in all neurons within a particular model. The individual inter-compartment coupling resistance is calculated from the geometry of the coupled compartments, using the global resistivity value. Thus if two cylindrical dendrites are adjacent compartments, the coupling resistance between them is the sum of half of the axial internal resistance of one dendrite, plus half of the axial internal resistance of the other dendrite. An important point is that although the internal resistance is calculated from the dimensions of the dendrites (length and cross-section area), and thus is in fact internal to the dendrite, in terms of the calculation it is treated as if it were external to the compartment. This is in accordance with the key underlying concept of compartmental models - that a compartment is isopotential (and thus has zero internal resistance).

Limitations
First I should make clear that Neurosim is not intended to be a fully-featured compartmental modelling solution. For such an activity I recommend specialist research programs such as Genesis or Neuron (but before worrying about ultimate accuracy I also recommend reading the review by Almog and Korngreen (2016) mentioned earlier).
Geometry
There are a number of simplifying assumptions made about compartment geometry. First, although a compartment may be designated as spherical (and drawn as a circle in the Setup view), it is in fact treated as an open-ended cylinder with the length equal to the diameter. This allows correct scaling of membrane-related structures (capacitance, channel conductance etc.) because the surface areas are the same (except for the missing patches of soma membrane where it connects to the axon or dendrites), but it takes no account of the varying cross-section of a sphere when calculating the internal resistance.
Second, compartments representing branch points in a dendritic tree are treated as simple cylinders (panel a below). This means that the calculated surface area of the compartment is probably inaccurate, as is the contribution of the branching structures to the coupling resistances. A more realistic representation (panel b below) would require more parameters to specify, and would be more complex to calculate.
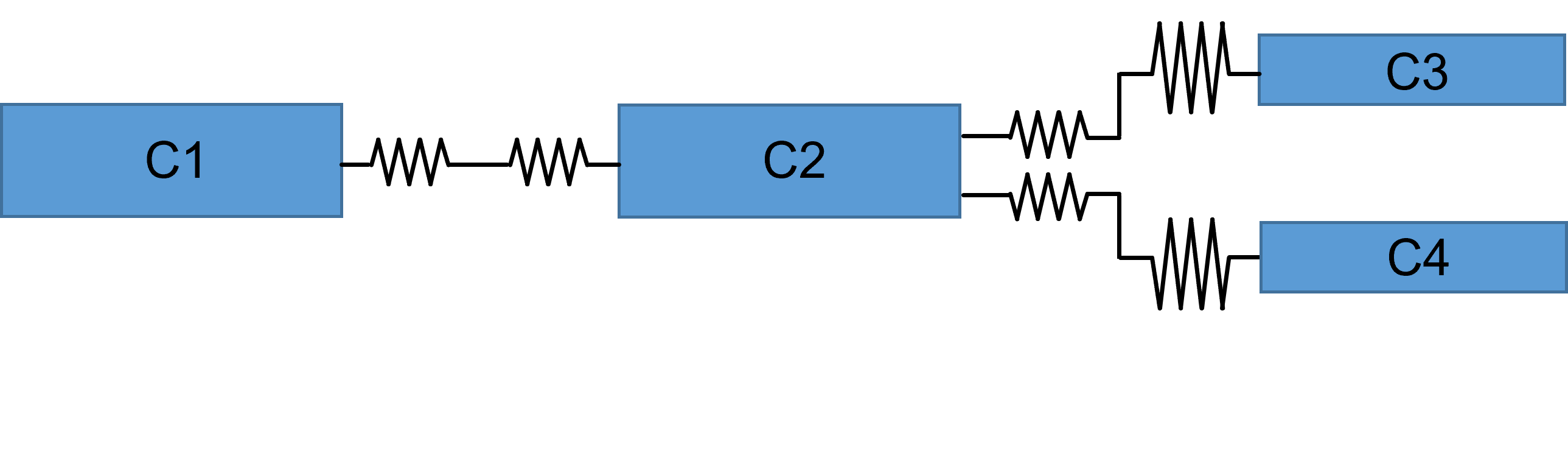
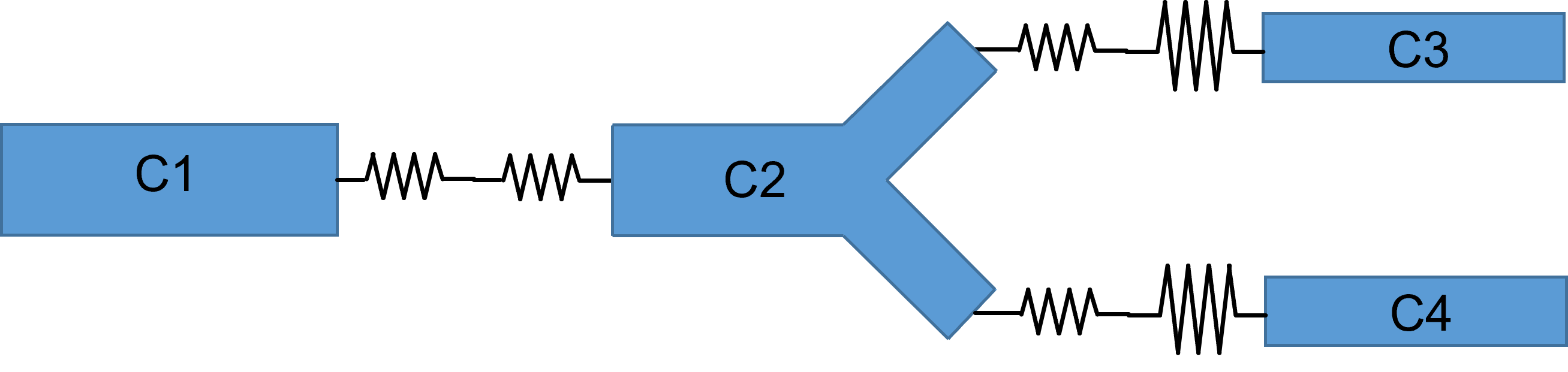
Third, the surface area of compartments at the ends of dendrites or the axon will be slightly underestimated, because all cylinders are treated as open-ended, with 0 surface area at the terminal end of the cylinder.
No Intracellular Ion Diffusion
Compartmental models can include simulation of changes in intracellular sodium or calcium concentrations, but there is no internal flow of these ions. Thus if chemical synaptic input occurs onto a particular compartment and the ion channel mediates calcium inflow, the resulting change in calcium concentration is restricted to the compartment receiving the input (although of course the current can spread throughout the entire neuron). A similar restriction occurs with voltage-dependent channels in which the carrier ion is designated as sodium or calcium.