Walk-Through: Build a Network

The Network module in Neurosim can simulate neural circuits containing an arbitrary number of neurons, linked by a wide variety of synaptic types. As an example, we will build a circuit that is loosely based on the auditory system of an owl – specifically, that part of the system that implements the Jeffress mechanism for localizing sound origin in the horizontal (azimuth) plane. This is investigated in detail in one of the Tutorials supplied with Neurosim, but in brief, the mechanism depends on the difference in the time of arrival of sound at the two ears (the inter-aural time difference, ITD) when the sound comes from an off-centre source. The time difference is computed using a combination of axonal delay lines and synaptic coincidence detection. See Sillar et al. (2016) for a recent review of the mechanism.

For your convenience (and to act as a reference if things go wrong during the build), the finished model is supplied in the Jeffress parameter file.

Warm Up

If you are new to Neurosim, it might be helpful to warm up with a quick tour of some editing features that you can use while building networks. There are MANY more editing facilities than are covered here, but this will get you started. Remember that you can press F1 at any point to open context-sensitive help within the program.

You can safely skip this section if you already know what you are doing.

Note that in the Setup view there are two neurons, N1 and N2, showing as yellow blobs. The blue diamond indicates a spiking chemical synapse (type a) from N1 to N2. N1 has 2 square boxes above it, which represent external stimuli.

In the following you will:

Follow these instructions:

That is how you move a single neuron and its associated connection to a new position in the Setup view. This does not change the circuit function at all, just the layout display.

When you release the mouse, both N1 and N2 are selected, and will be drawn with a thicker outline.

All the selected neurons move together.

A new neuron, N3, appears at the nearest grid to the location you clicked. This will have the properties of the most recently-added neuron.

This changes the post-synaptic neuron for this connection.

This changes lots of connection properties in one go.

This selects the two neurons individually, without having to drag around them.

This duplicates N1 and N3 as N4 and N5, and also the connection between N2 and N3, so N2 also connects to N5. The original neurons remain in place and selected.

This moves the stimulus. Note that in the Experimental Control panel (docked to the left of the Setup view), stimulus 2 becomes selected in the list, and the Target neuron shows as 3.

This just re-arranges the layout on the screen.

This duplicates the stimulus. Note that both N3 and N5 have a square stimulus 2 box attached to them, and that the Target neuron for stimulus 2 now shows 3 5. This indicates that the same stimulus will now be applied to both neurons 3 and 5, and if you were to change its properties (amplitude, duration etc.), the changes would apply to both neurons.

N2 disappears, along with its synaptic connections. The other neurons are re-numbered to fill the gap.

At this point you should have reciprocal synaptic connections between N1 and N2. However, the connecting lines overlap each other, so the circuit is a bit unclear.

This puts an angle node in the connecting line. You can drag the node to a new position, or you can delete it by right-clicking the node and selecting from the context menu. You can place as many angle nodes as you like in a connecting line.

This restores the circuit to its default condition.

IMPORTANT NOTE: Neurosim does not have an undo facility. So if you are building a complex network, it is a really good idea to save your work frequently, probably using a new name each time. This means that you can revert to an earlier version if something goes wrong.

Walk-Through

We now have just a single neuron in the circuit. (We could have also got here by selecting the Neuron: Delete all menu command.)

Coincidence Detection

Coincidence detection is at the heart of the Jeffress mechanism, so we will set this up first with just a single post-synaptic neuron.

Set up the neurons

First we will make two sensory neurons (one for each ear) plus one post-synaptic coincidence detector.

Set up the Results display

We now have three neurons, so we will set up the Results display so that we can see their activity.

You should see flat lines for all traces, since as yet absolutely nothing has been programmed to happen.

Note that if you save a file with data showing in the Results view, the data are saved too, which can make the file size much bigger. This is sometimes what you want, but in this case it would be pointless. So clearing the Results before saving is normally a good idea.

The next task is to set up coincidence detection. This requires some precisely-timed spikes in the sensory neurons, and synaptic connections to the coincidence detector.

Set up two pulse stimuli

In the Stimulus group of the Experimental Control panel note that the 0 (new) is selected in the list, and that the Target neuron(s) edit box is empty:

This applies a stimulus to N1, which should be visible in the Setup view as a square box attached to the neuron.

The response to the stimulus is visible, but subthreshold. We want the sensory neurons to be quite sensitive, so we will change their threshold.

This will “lock in” all values in the Properties dialog to the source neuron, which is N1. It will also apply any properties that have the box beside them checked to all neurons in the Extended Apply list. In this case there is only N2 in the list, but you could apply the threshold change to any number of neurons in the circuit.

We want to add another stimulus to N2. We cannot simply duplicate stimulus 1, because the new stimulus will need to have different properties.

A new stimulus, stimulus 2 is now applied to N2. Initially, it will have exactly the same properties as stimulus 1, but they can be edited separately.

We now have spikes in both the sensory neurons, N1 and N2, and we can control their timing. So we are now ready to set up coincidence detection.

Make the connections

At this point, the section of the Setup view should look like this:

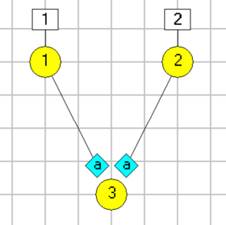
Coincidence layout 

Two EPSPs are visible in the post-synaptic coincidence detector (trace 3, green). However, they are quite small and rather long lasting. Even with 5 ms delay between the inputs, they show summation.

This will make the membrane of the sensory neuron a bit more leaky, thus reducing the time constant, and also making the EPSPs a bit smaller. The values were found by trial and error and work OK for this simulation.

The EPSPs are larger and briefer, although there is still some summation. But we can now test coincidence detection.

Because you did not clear the view between runs, the sweeps are overlaid. You could have checked the Auto clear box to clear before each sweep, but overlaid sweeps can be quite useful for comparison, and you can easily view them separately:

We are now in a situation where the summation of two EPSPs that are coincident crosses threshold and elicits a post-synaptic spike, but a 1 ms interval between the EPSPs in either direction fails to cross threshold. This is a good basis for coincidence detection.

Generate a Pure-Tone Auditory Stimulus

A brief pulse is an adequate representation of an auditory stimulus such as a click, but most stimuli involve ongoing noise. Furthermore, primary auditory neurons are frequency-specific. So we will change the stimulus to be more like a pure-tone sound.

We will apply a fairly low frequency sine-wave stimulus of 3 ms period (333 Hz) to the sensory neurons. Auditory sensory neurons respond to such stimuli with spikes that are phase-locked to the sine wave, but they do not spike on every cycle of the input. We want to reproduce this sort of behaviour.

In the Stimulus group of the Experimental Control panel:

Note in the Results view that the sensory neurons (N1 and N2) have identical responses, and both spike near the peak of the first sine wave. Their spikes are synchronous, and so the EPSPs in the post-synaptic neuron summate to produce a spike there too. The sensory neurons are silent for several cycles after the first spike, and then spike again. This is because of the relative refractory period after the first spike. This is a reasonable neural property, so we will leave it alone.

The stimulus onset is now earlier in the left neuron than the right, indicating a sound origin to the left of the midline. The spikes in the sensory neurons are no longer coincident, and the EPSPs in the post-synaptic neuron do not summate sufficiently to induce spikes.

You should now see both sine wave stimuli in the lower trace, as red and blue lines. They are in anti-phase with each other, because the difference in the delay times of the two stimuli is 1.5 ms, which is exactly half the sine wave period of 3 ms.

In a real nervous system, all neurons and all stimuli have some noise associated with them. In fact, noise is an essential feature of sensory systems that can actually improve their sensitivity (look at stochastic resonance in the tutorial section if you want more information on this). So we will add some noise to the sensory neurons.

Note that the membrane potentials of both N1 and N2 now shows some random variability, and occasionally spikes occur on the peak of a sine wave. You will probably see 2 or 3 spikes in each 30 ms simulation run. This seems about right for a just supra-threshold auditory stimulus. Each spike in either pre-synaptic neuron generates an EPSP in N3, but these are mainly subthreshold.

At this stage we have two neurons (N1 and N2) that perform a reasonable simulation of auditory afferents, and a working coincidence detector (N3). We now need to implement the Jeffress mechanism itself.

Jeffress Mechanism

We first need to create the coincidence detection layer: an array of neurons like just like N3 but with synaptic delays from each ear that increase by 0.2 ms as you progress along the array (this choice is somewhat arbitrary, but reasonable for this frequency). We will have 19 neurons in this layer in total. We want an odd number so that there will be a central neuron in the array, which will be the neuron that is activated best when the sound originates on the midline and arrives at both ears simultaneously. And 19 is a large enough number to show what we are interested in for this model, without being too unwieldy.

We could build the array by repeating the process described above for each extra neuron, but that would be quite tedious.

First we want to expand the layout area horizontally to make sure that there is enough room for the array.

Now we add the additional neurons.

This duplicates N3, including its synaptic connections. So we now have a new neuron N4, which also gets synaptic input from the sensory neurons N1 and N2. The input has the same delay (0 ms) as that to N3, but don’t worry about that. We can adjust it later.

You should now have 19 neurons in a line (N3 - N21). You may want to move the array to make the layout more accessible.

At this point your screen may look like this:

We have all the neurons we need, and we have them correctly connected to the sensory neurons, BUT the synaptic delays are all 0.

The easiest way to adjust a lot of connections where there is a straightforward pattern is to do it externally in a program like Excel.

The data should look like this:

Source

Target

Type

ID

Delay

Random factor

Gain modulator

1

3

1

a

0

1

1

2

3

1

a

0

1

1

1

4

1

a

0

1

1

2

4

1

a

0

1

1

1

5

1

a

0

1

1

2

5

1

a

0

1

1

Etc.

We want to replace the 0s in the Delay column with values which change by 0.2 ms between each neuron in the array. This can be done in Excel by sorting by the Source column, and then replicating values in the Delay column appropriately (note the change in direction when the Source changes from 1 to 2). You should end up with something like this:

Source

Target

Type

ID

Delay

Random factor

Gain modulator

1

3

1

a

0.2

1

1

1

4

1

a

0.4

1

1

1

5

1

a

0.6

1

1

1

6

1

a

0.8

1

1

1

7

1

a

1

1

1

1

8

1

a

1.2

1

1

1

9

1

a

1.4

1

1

1

10

1

a

1.6

1

1

1

11

1

a

1.8

1

1

1

12

1

a

2

1

1

1

13

1

a

2.2

1

1

1

14

1

a

2.4

1

1

1

15

1

a

2.6

1

1

1

16

1

a

2.8

1

1

1

17

1

a

3

1

1

1

18

1

a

3.2

1

1

1

19

1

a

3.4

1

1

1

20

1

a

3.6

1

1

1

21

1

a

3.8

1

1

2

3

1

a

3.8

1

1

2

4

1

a

3.6

1

1

2

5

1

a

3.4

1

1

2

6

1

a

3.2

1

1

2

7

1

a

3

1

1

2

8

1

a

2.8

1

1

2

9

1

a

2.6

1

1

2

10

1

a

2.4

1

1

2

11

1

a

2.2

1

1

2

12

1

a

2

1

1

2

13

1

a

1.8

1

1

2

14

1

a

1.6

1

1

2

15

1

a

1.4

1

1

2

16

1

a

1.2

1

1

2

17

1

a

1

1

1

2

18

1

a

0.8

1

1

2

19

1

a

0.6

1

1

2

20

1

a

0.4

1

1

2

21

1

a

0.2

1

1

WARNING: it is extremely easy to move a connection from one neuron to another when they are overlaid as closely as they are in this circuit. To avoid this risk, you may want to move (drag) a neuron out of the array line, so that its synapses are more easily isolated. You can move it back again once you have checked it.

Final Touches

Now it’s time to try it out.

Neurosim can display a maximum of 16 traces showing the membrane potentials of neurons, but in this case we are really only interested in the occurrence of spikes. So we will use a spike only display.

In the Results view:

The scrolling display shows a dot in the appropriate row every time the neuron for that row spikes. The top two rows show a high density of red and blue dots, which are the sensory neuron spikes. However, there is very little pattern to the remainder of the dots from the coincidence layer, which is a bit disappointing.

However, the frequency graph shows only very low frequency activity.

Now it is apparent that the frequency graph is not actually flat, so there is some pattern to the activity. But the overall activity level is only about 1 Hz in each neuron, which is very low indeed.
We need to get more excitation into the coincidence layer.

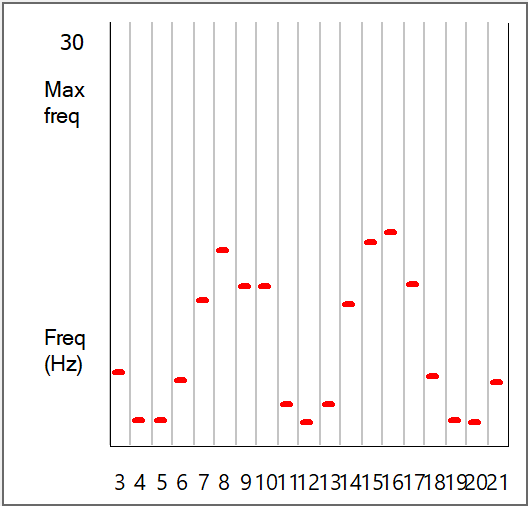
When the simulation ends, there is now a clear pattern to the coincidence layer activity in both the Results view and the Frequency graphs. There are two peaks of activity, centred around N8 and N16. This reflects the phase ambiguity that is evident in the Jeffress mechanism found in the owl nucleus laminaris brainstem region. This ambiguity persists right through to the behavioural level when the owl is given a pure-tone auditory stimulus, but disappears if the stimulus is white noise. The reasons for this are explored further in the main Tutorial section.

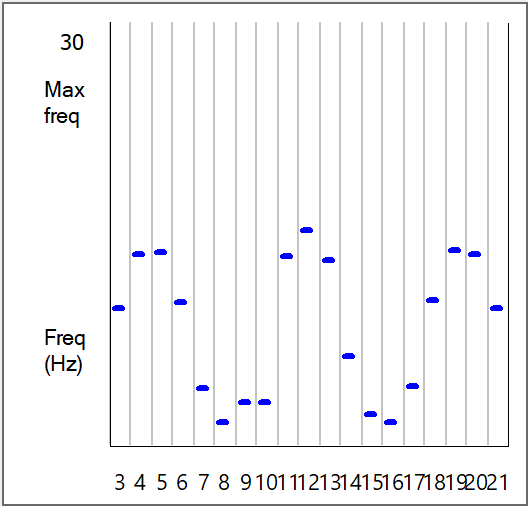
As a final check, let’s make the sound come from a midline source.

The peaks in the Frequency graph are now in different locations. The two graphs are shown below for comparison (left/above with red bars: sound origin offset, right/below with blue bars: sound origin midline). These graphs look very like published records of spike frequencies recorded from nucleus laminaris neurons in the owl when presented with pure-tone stimuli (e.g. Fig 12 in Carr and Konishi, 1990)

Offset sound source coincidence frquency                midline sound source coincidence frequency

Annotations and Images

It can be useful to add text annotations to the Setup view (or the Results view) to improve comprehension.

Another option on the context menu is to add an image. You have to have a suitable image, obviously, but you can add it to the view, and it will be save with the file along with all the other parameter settings.

NEXT

Copyright © W. J. Heitler (2019)