Tutorial Contents

Poisson from noise

Exponential intervals, Poisson counts

Departure from Poisson

Contents

Poisson from Noise

Sometimes neurons spike at fairly regular intervals, and this is called pacemaker activity. Sometimes neurons spike in fairly regular bursts, and this is called bursting activity. However, many neurons spike at highly irregular intervals, with no obvious pattern at all. Such activity is often described as a Poisson process - a series of events where the average time between events is fixed, but the exact timing of events is random. What is the origin of the randomness in such a neuron, and how does it lead to a Poisson process?

One of the core sources of random variability in the nervous system lies in the stochastic nature of the opening and closing of ion channels. In voltage dependent channels the transmembrane voltage affects the transition rate constants for opening and closing (at least in the Hodgkin-Huxley mechanism), and this in turn affects the likelihood of a channel being open. But it does this in a probabilistic, not deterministic, manner. Similarly in synaptic channels, ligand binding and unbinding, and channel opening and closing are all probabalistic events. It would be extremely difficult (probably impossible) to explicitly simulate the current generated by this channel noise, given the huge number of individual channels actually present a typical neuron. However, Linaro et al. (2011) showed by theoretical analysis that channel noise is an Ornstein-Uhlenbeck (OU) stochastic process. This effectively generates exponentially-filtered white noise, so there is random variability, but there is also autocorrelation in which successive samples depend to a greater or lesser extent on the value of the previous sample, with the extent determined by a time constant specified by the user. The output is quantitatively similar to the membrane noise shown by a "free running" neuron.

The file contains three traces. Trace 1 (upper) shows simulated neural activity generated externally by the program Neurosim. An integrate-and-fire neuron has membrane noise generated by the OU process with a time constant of 5 ms. The membrane periodically and randomly crosses threshold and generates a spike. The spikes were detected by threshold crossing, and are marked in event channel a. Trace 2 (middle) just shows white noise with successive values drawn randomly from a standard normal distribution (mean = 0, standard deviation = 1). For this trace, events were detected by positive threshold-crossing with a level set to 2.5, and stored in channel b. Trace 3 (lower) also shows noise, but this time the values are drawn from a uniform random distribution (0 <= x < 1). Events were detected with a threshold of 0.99.

You can now see the difference between the traces more clearly. The upper trace has the strong serial correlation characteristic of an OU process, and of the membrane potential of a real neuron. The middle and lower traces have no serial correlation.

Exponential Intervals, Poisson Counts

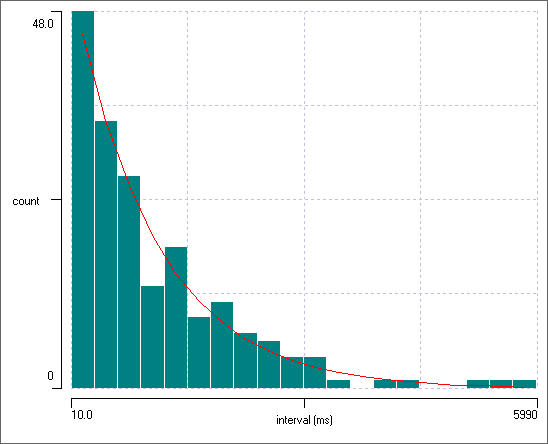
The histogram shows a declining series of data bins whose peaks are a fairly good fit to an exponential PDF (probability distribution function: the red line). The mean value in the histogram is 1066 ms, and standard deviation of the values is 1061 ms. Thus the mean and standard deviation have similar numerical values, which is exactly as it should be for an exponential distribution.

At this point it might seem slightly puzzling that we are seeing an exponential distribution generated by what we assume is a Poisson process. However, this is not a problem. It can be shownOr so I am told. I don't know how to do this personally. mathematically that if the number of events occurring within a series of fixed time intervals follows a Poisson distribution, than the length of time between each of the events (the interval) will follow an exponential distribution. The default histogram shows the interval between events, hence the exponential distribution.

The histogram now shows the "textbook" skewed distribution characteristic of the Poisson PDF. The analysis divides the data into a consecutive series of binsThese bins have nothing to do with the bin width on the histogram itself. (segments), each 2000 ms in length, and counts how many events occur in each segment and displays the results as a histogram. The left-most histogram bin has a height of 15, and this means that there are 15 2000 ms-length non-overlapping segments in the data that have no events in them. The next bin tells us that there are 31 segments with 1 event in them. This is the modal value of the histogram. The right-most bin tells us that there are 2 segments that have 6 events in them, and these are thus the segments with the highest local frequency of spikes. (Of course, the histogram does not tell us which these segments are - for that you would have to set up a consecutive series of 2000 ms events in another channel, and use a scattergraph to plot the event IDs or onset times of events in that chanel against the number of events in the spike channel that occurred within each enclosing event.)

Note that the Poisson distribution is a discrete distribution because the counts can only take integer values. This is why the red Poisson PDF is drawn as a series of steps superimposed on the histogram. In contrast, the exponential distribution is a continuous distribution because it refers to time values that can have any fractional value. That is why the exponential PDF was drawn as a curve.

a
Exponential interval distribution
b
Poisson distribution of counts
A Poisson process. a. The inter-event interval follows a continuous exponential distribution. b. The event count within consecutive time bins of specified duration follows a discrete Poisson distribution.

Now look at the distribution of events generated by trace 2, the standard normal distribution.

Again we see the skewed histogram characteristic of a Poisson distribution. The discrete PDF is an almost exact match to the underlying histogram bins.

Trace 3 is drawn randomly from a uniform distribution, so it has very different statistical properties to trace 2 which drawn from a normal distribution. However, the threshold-crossing probability count still follows a Poisson distribution. It appearsI say "appears" because I am not a good enough mathematician to know if this is an absolute truth. But it certainly holds for these data. that applying a threshold to a random process, irrespective of the random distribution, generates a Poisson distribution of counts and an exponential distribution of intervals.

Note that the visual appearance of the skew in the classic Poisson histogram is highly dependent on the distribution bin (segment) length:

With the longer Distrib bin value there are more counts in each segment and the histogram looks quite similar to a normal (Gaussian) distribution. This is to be expected, because if the expected average count per segment is greater than about 10, the Poisson distribution PDF approaches that of a normal distribution. However, with this setting, the BIC and likelihood values indicate that the data are still a better fit to a Poisson than Gaussian distribution (see the Event Histogram tutorial for a description of likelihood and BIC).

Departures from the Poisson Distribution

Although spikes that are driven by unpatterned random input are often modelled as following a Poisson distribution, it is unlikely that they will follow one exactly. One reason for this is that a pure Poisson process has absolutely no "memory" - the probability of occurrence of an event is completely independent of the time since the previous event. With real neurons this is clearly not the case. The absolute refractory period means that there is a "dead space" period after a spike occurs during which another spike cannot occur, and this is followed by the relative refractory period in which the probability of another spike is reduced, although non-zero. A further complication is that the serial correlation typically shown in the variations in membrane potential means that a depolarized potential (and therefore an elevated spike probability) at one moment in time is likely to be followed by a period of further depolarized potential and further elevated probability. The importance or otherwise of this effect obviously depends on the timescale of serial correlation.

However, the simulation underlying trace 1 has membrane potential variability that shows serial correlation, and spikes that have both absolute and relative refractory periods, and yet the spike distribution still shows a good approximation to a Poisson process. So although the mechanism underlying the spike distribution variability may not exactly meet the formal mathematical constraints of a Poisson process, the statistical description of the variability as such a process is still a very useful shorthand.