Condensation of Excitons and Polaritons

Excitons and Polaritons

Excitons are excitations in semiconductors, consisting of a bound electron and hole (missing electron); they may be created by shining light on a semiconductor, exciting an electron to a new excited state; both the electron and the hole corresponding to the old state of the electron can move about independently, but because of electric interactions, the electron is attracted to the hole, and they may form a bound state. In appropriately engineered systems, such as coupled quantum wells — thin layers of differing semiconductor, choosen to trap electrons or holes — excitons can be made relatively stable and have a significant lifetime.

Microcavity polaritons are mixtures of photons (quantised particles of light) and excitons ; this mixing is achieved using mirrors to build a cavity that confines light, and placing a quantum well that confines excitons between these mirrors.

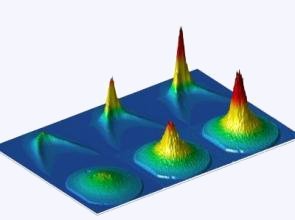
Polariton occupations

Occupation of different energy/momentum states across the condensation threshold for microcavity polaritons: left-most case is uncondensed, right-most is condensed. The further set of images show occupation versus energy and momentum, the nearer show occupation versus two components of momentum. [Adapted from Kasprzak et al, Nature 443 409 (2006)]

Condensation

Condensation in this context refers to a phase transition, generally at low temperatures, below which the quantum system behaves coherently; roughly one may think of this as all particles behaving identically; i.e. many particles occupying the same quantum mechanical wavefunction. It is this coherence, resulting from sharing the same wavefunction, that means quantum mechanical effects may become visible on large scales

Examples of such condensates include superconductivity (where there is flow of current without electrical resistance) and superfluidity of liquid Helium (where there is fluid flow without mechanical resistance). Superconductivity and superfluid Helium are however somewhat exceptional as quantum condensates: they are the true equilibrium states of the given material. The last decade has seen an increasing range of other quantum condensates in systems which are not in perfect equilibrium. These include cold dilute gases of alkali atoms and very recently condensates of quasi-particle excitations in semiconductors, microcavity polaritons

Microcavity polaritons can form quantum condensates at much higher temperatures than the cold atomic gases, but are further from equilibrium due to the finite lifetime of the polaritons. While the equilibrium condensate, and the highly non-equilibrium laser have been extensively studied, exploration of systems between these two limits have has only begun recently.

Vortex lattice formation

Spontaneous formation of a rotating vortex lattice in a pumped decaying condensate. [Adapted from Keeling and Berloff, Phys. Rev. Lett 100, 250401 (2008)]

Non-equilibrium

One particular area of interest is in understanding how the properties of condensates consisting of particles with finite lifetimes differ from these two extreme limits of the Laser and the equilibrium condensate. My work to date has addressed questions about: how correlation functions, studying the coherence between polaritons in different places, are modified; how spatial structure, such as seen in the adjacent figure, becomes modified; and how the conditions required for condensation change.

Recent articles on polaritons

  1. Coherently driven microcavity-polaritons and the question of superfluidity R. T. Juggins, J. Keeling, and M. H. Szymańska Nat. Commun. 9 4062 (2018) (DOI: 10.1038/s41467-018-06436-2)
  2. Efficient non-Markovian quantum dynamics using time-evolving matrix product operators A. Strathearn, P. Kirton, D. Kilda, J. Keeling, and B. W. Lovett Nat. Commun. 9 3322 (2018) (DOI: 10.1038/s41467-018-05617-3)
  3. Orientational alignment in cavity quantum electrodynamics J. Keeling and P. G. Kirton Phys. Rev. A 97 053836 (2018) (DOI: 10.1103/PhysRevA.97.053836)
  4. Exact States and Spectra of Vibrationally Dressed Polaritons M. A. Zeb, P. G. Kirton, and J. Keeling ACS Photonics 5 249 (2017) (DOI: 10.1021/acsphotonics.7b00916)
  5. Raman scattering with strongly coupled vibron-polaritons A. Strashko and J. Keeling Phys. Rev. A 94 23843 (2016) (DOI: 10.1103/PhysRevA.94.023843)
  6. Excitonic spectral features in strongly coupled organic polaritons J. A. Ćwik, P. Kirton, S. De Liberato, and J. Keeling Phys. Rev. A 93 033840 (2016) (DOI: 10.1103/PhysRevA.93.033840)
  7. Polariton condensation with saturable molecules dressed by vibrational modes J. A. Ćwik, S. Reja, P. B. Littlewood, and J. Keeling Eur. Lett. 105 47009 (2014) (DOI: 10.1209/0295-5075/105/47009)
  8. Non-Equilibrium Bose-Einstein Condensation in a Dissipative Environment M. H. Szymanska, J. Keeling, and P. B. Littlewood p. 447 of Quantum Gases Finite Temp. Non-equilibrium Dyn. (2013) Eds. N. P. Proukakis, S. Gardiner, M. J. Davis, and M. H. Szymanska (DOI: 10.1142/9781848168121_0030)
  9. Universality in Modelling Non-equilibrium Pattern Formation in Polariton Condensates N. G. Berloff and J. Keeling p. 19 of Phys. Quantum Fluids (2013) Eds. A. Bramati and M. Modugno (DOI: 10.1007/978-3-642-37569-9)
  10. Power-law decay of the spatial correlation function in exciton-polariton condensates G. Roumpos, M. Lohse, W. H. Nitsche, J. Keeling, M. H. Szymanska, P. B. Littlewood, A. Löffler, S. Höfling, L. Worschech, A. Forchel, and Y. Yamamoto Proc. Natl. Acad. Sci. 109 6467 (2012) (DOI: 10.1073/pnas.1107970109)
  11. Spatial pattern formation and polarization dynamics of a nonequilibrium spinor polariton condensate M. O. Borgh, J. Keeling, and N. G. Berloff Phys. Rev. B 81 235302 (2010) (DOI: 10.1103/PhysRevB.81.235302)
  12. Polarized polariton condensates and coupled XY models J. Keeling Phys. Rev. B 78 205316 (2008) (DOI: 10.1103/PhysRevB.78.205316)
  13. Spontaneous Rotating Vortex Lattices in a Pumped Decaying Condensate J. Keeling and N. G. Berloff Phys. Rev. Lett. 100 250401 (2008) (DOI: 10.1103/PhysRevLett.100.250401)

Time dependent cavity quantum electrodynamics

Collapse and revival of photon field strength

Collapse and revival of photon field amplitude as a function of rate of energy variation. [Adapted from Keeling and Gurarie, Phys. Rev. Lett 101 033001 (2008)]

In order to investigate the potential behaviour of non-equilibrium quantum systems, it is useful to have particularly simple and well controlled systems where these ideas can be explored. One of the simplest realisable quantum systems where interesting behaviour can be seen consists of two-level atoms (i.e. an atom modelled as having only two internal states) coupled to electromagnetic radiation in a cavity. This model system has long been used as a textbook example from where one may start to understand the quantum nature of coupling between light and matter. However, recently, it has also become an experimental reality, allowing one to also study to what extent textbook ideas can be translated into these model systems. This is particularly important in understanding whether idealised descriptions of using quantum systems for information processing will survive the imperfections of the real system.

One interesting question in this context is to explore what happens to the dynamics of such systems, when one subjects them to time dependent fields. The figure is an illustration of one such questions, studying how the light field in the cavity responds to a time varying static electric field applied to the two-level atom. I have also worked on the dynamics of such systems (with many atoms), when starting from high excited states, studying in particular those cases where the classical equations of motion dramatically fail to describe the subsequent dynamics.

Dynamics and realisations of the Dicke model

Cold atoms in an optical cavity

Cartoon figure of cold atoms interacting with light in an optical cavity, as well as a perpendicular pump laser. [Adapted from Keeling et al. Phys. Rev. Lett. 105 043001]

For large numbers of atoms in close proximity, one can see collective effects — behaviour that is not describable by each atom acting independently. This idea was first discussed by Dicke, who considered the rate of emission of radiation of initially excited atoms, when radiating into free space. When large numbers of atoms are instead placed in a cavity, the simplest model of interaction between atoms and light would suggest they can have an even more dramatic effect; i.e. above a certain density, the atoms would spontaneously polarise and start generating a self-consistent electric field to maintain their polarisation.

Phase diagram

Phase diagram as a function of effective pump detuning (horizontal) and pump strength (vertical) [Adapted from Keeling et al. Phys. Rev. Lett. 105 043001]

For real atoms in an optical cavity, this idea does not work, as the limitations of the model become relevant under the same conditions where the transition might be expected. However, the transition can be made to happen in other systems, where the model as originally conceived can in fact be applied. One instance of this concerns cold atoms in an optical cavity, pumped by a perpendicular laser beam [See Baumann et al. Nature 464, 1301 (2010)], as illustrated to the left. In this case, the transition corresponds to a jump in the intensity of light in the cavity mode, as one varies the strength and frequency of the pumping laser.

While the basic idea of the transition in this system can be reduced to a well studied model, differences between the actual system and the idealised model can in this case lead to novel polarised states, including regions where multiple phases exist simultaneously. These systems potentially allow one to explore the collective dynamics of a non-equilibrium quantum system, and thus gain insight into the range of states such pumped systems can display.

Recent articles on the Dicke model

  1. Sign-Changing Photon-Mediated Atom Interactions in Multimode Cavity Quantum Electrodynamics Y. Guo, R. M. Kroeze, V. D. Vaidya, J. Keeling, and B. L. Lev Phys. Rev. Lett. 122 193601 (2019) (DOI: 10.1103/PhysRevLett.122.193601)
  2. Emergent and broken symmetries of atomic self-organization arising from Gouy phase shifts in multimode cavity QED Y. Guo, V. D. Vaidya, R. M. Kroeze, R. A. Lunney, B. L. Lev, and J. Keeling Phys. Rev. A 99 53818 (2019) (DOI: 10.1103/PhysRevA.99.053818)
  3. Atom-only descriptions of the driven-dissipative Dicke model F. Damanet, A. J. A. Daley, and J. Keeling Phys. Rev. A 99 033845 (2019) (DOI: 10.1103/PhysRevA.99.033845)
  4. Spinor Self-Ordering of a Quantum Gas in a Cavity R. M. Kroeze, Y. Guo, V. D. Vaidya, J. Keeling, and B. L. Lev Phys. Rev. Lett. 121 163601 (2018) (DOI: 10.1103/PhysRevLett.121.163601)
  5. Generalized classes of continuous symmetries in two-mode Dicke models R. I. Moodie, K. E. Ballantine, and J. Keeling Phys. Rev. A 97 033802 (2018) (DOI: 10.1103/PhysRevA.97.033802)
  6. Tunable-Range, Photon-Mediated Atomic Interactions in Multimode Cavity QED V. D. Vaidya, Y. Guo, R. M. Kroeze, K. E. Ballantine, A. J. Kollár, J. Keeling, and B. L. Lev Phys. Rev. X 8 011002 (2018) (DOI: 10.1103/PhysRevX.8.011002)
  7. Superradiant and lasing states in driven-dissipative Dicke models P. Kirton and J. Keeling New J. Phys. 20 015009 (2018) (DOI: 10.1088/1367-2630/aaa11d)
  8. Suppressing and restoring the dicke superradiance transition by dephasing and decay P. Kirton and J. Keeling Phys. Rev. Lett. 118 123602 (2017) (DOI: 10.1103/PhysRevLett.118.123602)
  9. Dynamics of nonequilibrium Dicke models M. J. Bhaseen, J. Mayoh, B. D. Simons, and J. Keeling Phys. Rev. A 85 013817 (2012) (DOI: 10.1103/PhysRevA.85.013817)
  10. Collective dynamics of bose-einstein condensates in optical cavities J. Keeling, M. J. Bhaseen, and B. D. Simons Phys. Rev. Lett. 105 43001 (2010) (DOI: 10.1103/PhysRevLett.105.043001)

Creating controlled electron pulses in 1D wires

Real space pciture of current pulse

Schematic diagram of density of electrons, holes, and total charge within a pulse, after application of a time-dependent voltage

When a voltage is applied to a conducting wire, a current results. However, in most cases, far more electrons are excited than are necessary to create this current. Instead, excited electron hole pairs are also created, and so the description of the state of the wire following an arbitrary voltage is quite complicated.

However, it turns out that there are ways in which one can insert a single electron into a wire without the creation of additional electron hole paris. This can for example be done by applying a lorenzian voltage pulse, or by coupling the wire to a quantum dot storing a single electron, and then varying the energy of the dot with the correct time dependence. In both these cases, quantum mechanical interference can cause a cancellation that prevents excitations being created.

This system again allows one to explore non-equilibrium quantum dynamics in a driven system, but one involving electrons, rather than photons, and consequently showing a quite different variety of behaviour.