
You all know that if you place a plank on a log, a lightweight person standing at one end of the plank can balance a heavy person standing at the other, so long as the log is offset to one side.

This is because the plank acts as a lever, in which the log is the pivot point. More specifically, the plank acts as a first-order lever.
The fundamental equation for levers is very simple:
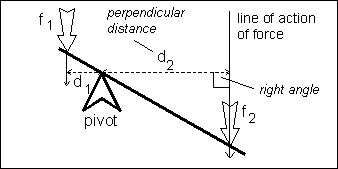
\begin{equation} f_1d_1 =f_2d_2 \end{equation}where f1 is the force (or weight) on one side of the pivot and d1 is the perpendicular distance between the line of action of the force and the pivot. Similarly, f2 and d2 are the equivalent values on the other side of the pivot.

The "perpendicular distance between the line of action of the force and the pivot" is a bit of a mouthful, but it means a line drawn from the pivot which meets the direction of thrust of the force at right angles. Thus if the lever is not horizontal it looks like this:
Now let us look at how this applies to the extensor tibiae muscle and the leg.
When the tibia is half extended, the situation is just like the first lever diagram above, except tilted sideways. The "heavy person" is the extensor muscle tendon, pulling on a short lever of 0.63 mm. The "light person" is the end of the tibia, pushing on the ground through a long lever of 22 mm.
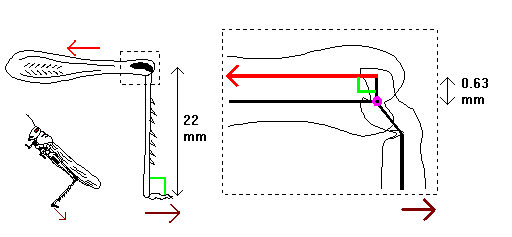
In the half-extended position the extensor muscle pulls at 90o relative to the tibia, and with a take-off angle of 45o (small picture), the tibia is angled at 90o relative to the thrust vector on the ground. This means that the extensor muscle has the best possible mechanical advantage (about 1 to 35) in terms of producing the most thrust from the tibia for a given muscle force. (It might be better called a mechanical disadvantage, since the muscle has to produce 35 times more force than is actually applied to the ground to accelerate the grasshopper - but it is still the best that can be achieved given the geometry of the leg.)
When the tibia is fully flexed the extensor muscle no longer pulls at 90o relative to the tibia, although the tibia is still angled at about 90o relative to the ground.
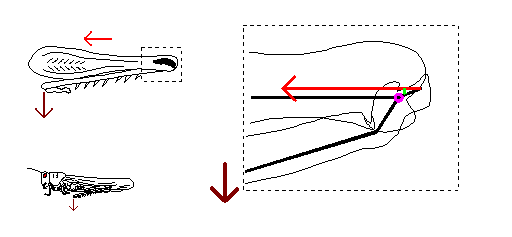
In the fully flexed position the extensor muscle pulls at less than 7o relative to the tibia. This gives the extensor muscle a mechanical advantage relative to the ground of between 1 : 150 and 1 : 260 (it is hard to measure accurately). and the muscle has to produce a very great deal of force in order to produce a quite modest thrust on the ground.
At the start of the jump, each leg pushes on the ground with a force of about 0.05 N, which means that the muscle must be producing a force of 10 - 15 N.
Remember that 1 N (newton) is about 100 g, so with both legs pushing, the total force is about 10 g, which is more than enough to start to lift a 3 g grasshopper. Then the force increases as the mechanical advantage improves as the leg extends.
Close