Rhythm Analysis Helper

A common task in some areas of neuroscience is to analyse rhythmic activity such as locomotion or respiration. DataView has various facilities to help such analysis: this tutorial describes one of them.

• Load the file tadpole rhythm.

This shows a fragment of extracellular recording from a spinal motor root during an episode of swimming in a tadpole. The activity consists of bursts of spikes which are obviously rhythmic. The aim is to analyse the main characteristics of the rhythm such as its frequency, burst duration, duty cycle etc. The first task is to mark the activity with events, since these are what will form the basis for analysis.

Detect Activity as Outliers

• Select the Event edit: Threshold menu command to open the Threshold dialog.
• Select Mean +/- sd x mult as the Threshold source.
• Select Least active as the Traces stats source, leaving the window at the default value of 10 ms.
• Select +/-ve from the Threshold Onset group.
  The bursts in the rhythm have both negative and positive deflections, so it makes sense to detect them both.

At this point the dialog should look like this:

• Click Analyse and then Close the dialog.

You now have events marking each positive-going "outlier" excursion of the recording, where outlier is defined in terms of the background noise. [See here for more details.]

Helper Dialog

• Select the Event analyse: Rhythm analysis helper command to activate the Rhythm analysis helper dialog box. This is a non-modal dialog, so you can switch away from it and interact directly with the main display if you wish.

This dialog box is intended to help you detect and analyse rhythmic activity. All the facilities within the dialog are available elsewhere as stand-alone options, but the dialog combines them into one location and adds some facilites for integrating and automating the separate stages.

At the left side is a frame labelled Rhythm, in which you select both the Chan which holds or will hold the rhythm, and the Mode for rhythm detection. Initially, the Rhythm chan is set to an empty event channel (in this case b), so the dialog box does not show anything interesting. There are four modes in which the Rhythm analysis helper can be used:

Merge-drop filter: The Merge/drop filter applies a minimum off-time filter followed by a minimum on-time filter to events in a Source channel (specified in the right-hand Analysis: Merge/drop frame), to derive events which are written into the Rhythm channel. This means that close-together events in the source channel, which are likely to derive from bursts in the rhythm, get merged into single events, while any remaining short events after this process are likely to derive from ectopic spikes or noise, and get eliminated.

Poisson surprise: This applies the Poisson surprise method to detect bursts in the Source channel and again these are written into the Rhythm channel. See here for details of the method.

Hill-valley: This mode writes events into the Rhythm channel which encompass each “hill” in a selected data trace, optionally excluding small hills ("molehills"). This is normally applied after rectifying and smoothing data. See here for details of the method.

Direct: This mode looks for rhythms which are already directly present in the Rhythm event channel, without reference to any source channel or trace.

Merge-Drop Filter

We will apply the default Merge/drop filter on events detected by threshold crossing in Source channel a, to try to extract the rhythm into Rhythm channel b. There are two ways to go forward; we can set the filter parameters manually by trial-and-error, or we can try to automatically detect a suitable set of parameters. We will first try the manual method because this will help to make clear how the analysis works. We will then try the automatic method, to see whether it yields similar results.

Note that some of the information supplied in this section (e.g. about the graphs and outliers) applies to the other analysis modes as well.

Minimum Off-Time

The filter characteristics are set in the right-hand Analysis: Merge/drop frame in the dialog box.

• Click the Analyse button in the Analysis frame.

Initially, there is no filtering (Min off-time and Min on-time are both set to 0), and the 2927 events in channel a are simply replicated into channel b. There are 3 graphs in the lower part of the dialog box. The left-hand graph is a scatter-plot showing the instantaneous frequency of Rhythm events plotted against time. The middle graph is a scatter-plot showing the width (duration) of Rhythm events plotted against time. The right-hand histogram can show a variety of things depending on the selection in the drop-down list, but the default is the distribution of the durations of off-times, i.e. the times between the end of one event and the beginning of the next.

Note that the histogram shows a large peak of very short times at the left-hand edge, and a smaller distributed peak of longer times. The short-time peak is due to the clusters of close-together events within a burst of the rhythm, the longer times are the times between bursts. You can get a better view of the longer times by checking the Log Y box just above the histogram, but once you have tried this, uncheck it to return to the linear (non-log) view.

• Now click the up-arrow spin button of the Min off-time edit box.

This increases the value in the box to 1 ms, which means that adjacent events in the Source channel which are separated by an off-time of 1 ms or less are merged together in the Rhythm channel. You can see this in the main Chart view. Note that the number of events in the Rhythm channel decreases to 785, and that a frequency trend starts to become visible at the bottom of the left-hand (frequency) scatter plot in the dialog.  

Also note that a red vertical cursor is visible at the left-hand edge of the right-hand off-time histogram. This shows the value of the min off-time on the histogram, and it can be dragged by the mouse as an alternative way to set the min off-time rather than using the edit box. However, for now keep using the spin buttons on the edit box.

• Keep increasing the min off-time until it reaches a value of 6 ms, at which point the dialog should look like this:

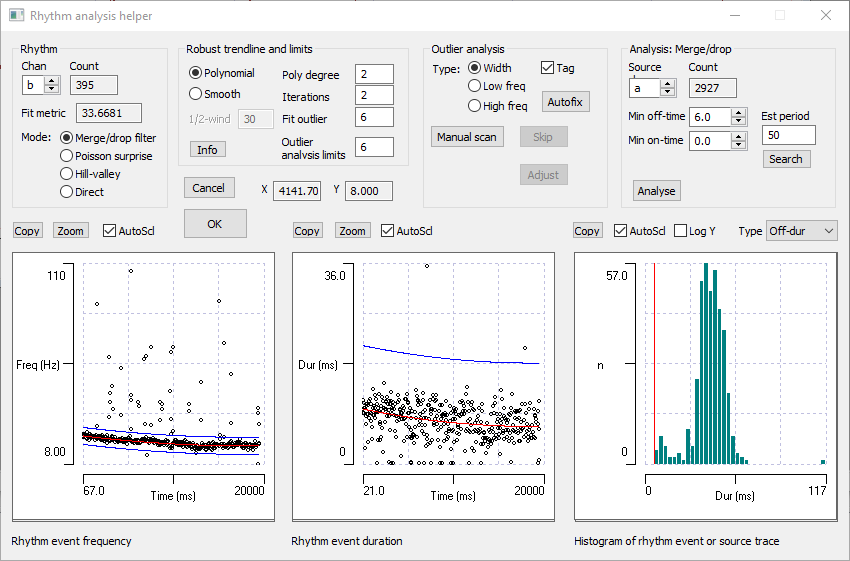
The graphs now look rather better. The frequency (left-hand) graph shows a very clear pattern of slightly declining frequency, with a red trendline drawn through it. There are also blue limit lines drawn above and below the trendline, which define the excursion beyond which points are regarded as outliers. There are a couple of low-frequency outliers, and rather more (but still not too many) high-frequency outliers. The duration (centre) graph also shows a clear pattern, with most events having widths of 6 - 9 ms. (If you hover the mouse over any graph, the X and Y values at that point are displayed in the edit boxes beside the Cancel button.)

The Robust Trendline and Outlier Limits

The trendline and confidence limits are drawn according to parameters set in the Robust trendline and limits panel, using a LOWESS procedure. If the data follow a fairly smooth curve as is the case here, then a polynomial fit is probably appropriate, but if the data follow a more complex pattern, then smoothing might be better. The poly degree parameter sets the degree of the fit (where 0 is a simple average). The Iterations affects the degree of robustness – the higher the value, the less influence outliers have. The Fit outlier def sets the threshold value (as a multiple of the median absolute deviation [MAD] from the median) beyond which outliers have no influence on the fit. The smaller this value, the less influence outliers have, so this too affects the robustness. The Outlier analysis limits sets where the blue confidence limits are drawn on the graphs as a multiple of the MAD. You would normally set the same value for the outlier definition and the confidence limits, but you don’t have to. The ½ wind sets the size of the window used if you choose the Smooth rather than Polynomial option. The larger the window, the greater the degree of smoothing.

If you click on any point in either scatter-plot, the corresponding event in the pattern channel will be centred in the main view.

• Click on the highest outlier in the frequency graph (the point at the top of the graph very close to the first grid line: ~ 5100 ms, 97 Hz).

This should centre event 123 (in the Rhythm channel b) in the main display. Note that the preceding event 122 is rather close to 123, hence the high frequency. However, event 122 is very brief, and is probably a spurious event caused by a random threshold crossing.

We could explicitly delete event 122 using the standard event edit methods, but at this stage leave it be.

Now set the Min off-time to 30 ms. Many of the high outliers disappear from the frequency graph, but now there are rather more low outliers, and more high outliers have appeared in the duration (centre graph). If you look at the main display you will see that the previous events 122 and 123 have now merged (to form a new event 110), as have the preceding two bursts (now forming event 109). This is because the off-time between them was less than 30 ms. This is not good, because event 109 is obviously made from 2 separate bursts. So set the Min off-time back to 6 ms.

Minimum on-time

• Select On-dur from the drop-down list above the hisogram. The histogram now displays the durations of the Rhythm channel events. There is a possible discontinuity at the left-hand side, with a peak in the first histogram bin, and then a trough before the main cluster.
• Set the Min on-time edit box to 1 ms.

The programme now applies the two filters sequentially. First all events in Source channel a separated by less than the minimum off-time of 6 ms are merged and copied into an internal holding channel. Second, all remaining events in Source channel which are longer in duration than the minimum on-time are copied into the holding channel, while events in the Source channel which are of shorter duration than the minimum on-time are ignored. Finally, the holding channel is copied into the Rhythm channel.

After this double filter process, we have now got rid of many of the high outliers from the frequency graph.

• Click on the bottom-right low outlier in the frequency graph (~ 19000 ms, 9 Hz) to centre event 373.

There is a brief drop-out in the recording which occurs at the time that a previous burst would have been expected. This is an obvious glitch in the recording, and has no scientific significance.

• Click on the highest outlier in the middle duration graph (~ 7000 ms, 36 ms) to centre event 151.

This appears to be another glitch in the recording, where some spurious noise has extended a burst duration. (Note that this also generates a high-frequency outliers, since the interval between events 150 and 151 is shorter than usual).

At this point you would probably stop the analysis in a real experiment. You can get listings of the actual values (frequency and duration) using the standard Event analyse: List/save event parameters command. If you click the Info button in the Robust trendline and limits panel, a dialog will display showing the median absolute deviation (from the median) (MAD) of data in the two scatter-plots, and the coefficients of the robust polynomial trendlines of the plots. Thus, in this case the coefficients indicate that the frequency trendline follows the quadratic equation:

y = 22.8 - 5.75*10^-4x + 1.65*10^-8x²

The advantage of stopping at this point is that the procedure so far is entirely repeatable. No “hand tuning” has been done on individual events, so the rules devised for this analysis (threshold at 5 times the standard deviation of the noise, minimum off-time of 6 ms, minimum on-time of 1 ms) could be applied to similar experiments, with, for instance, various drugs applied. However, if you wanted to refine the plots further, you have two options. You could click on individual outliers, and hand-edit events in the main display, or you could use the facilities in the Outlier analysis panel within this dialog.

Outlier Correction

Outlier analysis occurs in three stages – width outliers, low-frequency outliers and high-frequency outliers, as determined by the radio buttons within the Outlier analysis panel. There is an Autofix button, which will attempt to automatically fix all outliers of the selected type, but it is probably safer to do a Manual scan, at least for fairly small files.

Width outlier correction

• With the Width outlier type selected, click the Manual scan button.

The main display centres the first width outlier (event 151), and draws 2 vertical cursors around the “suggested” fix. To suggest a fix the programme looks for a cluster of events within the Source channel (a) which would yield a Rhythm event at a time that would give an appropriate frequency, and with a duration that would not be an outlier.

The outlier event in this case is caused by an electrical “glitch” in the recording that has produced spurious threshold crossings. However, the programme has made a good guess for a fix. The cursors are placed to bracket what looks like the “real” burst. Look at the width (centre) graph, and note that the highest outlier is outlined in blue, while a point in red appears just below the trendline and well within the outlier limits. The blue point is the width (outlier) point that will disappear, and the red point is the new width that will appear, if we accept the fix. Now look at the frequency graph (left), and note that two outlier points are outlined in blue, and two points appear in red. Again, the blue points are frequencies that will disappear if we accept the fix, while the red points are new frequencies that will be generated. Thus fixing the width outlier not only fixes the width problem, but also removes both a high and low frequency outlier!

Also note that a green tick appears beside the Adjust button, indicating that if the suggested fix is accepted by clicking the button, no new outliers will be generated.

If you did not like the suggested fix, you could adjust it by dragging the cursors on the main display.

• Drag the left-hand cursor leftwards, to just after the big downwards “glitch”. Note that the green tick disappears, because although the new suggested fix slightly improves the outliers, it does not remove them (the red points are outside the limit lines on the graphs).
• Drag the cursor back to where it was before (or click Stop scan and then Manual scan to restart the process and get the cursor back to exactly where it was before).
• Click Adjust (you could click Skip if you decided not to change the outlier).

A point to note when you drag the cursors to adjust a suggested width fix is that the width always changes in steps dictated by the events in the Source channel when you are in Min off-on filter or either of the surprise modes. If you were in the fourth mode, Direct, then the fix would directly reflect the actual positions of the cursors.

The scan advances to the next (and last) high duration outlier. This is caused by a small potential late in the burst that just crossed threshold. It could be eliminated by clicking Adjust, but it is a matter of judgement whether it should be adjusted. My (strongish) opinion is that it should not. The previous outlier was obviously caused by an artefact, this one is caused by genuine data. If we did not like the result, it would be better to adjust the initial threshold settings in event detection, to keep the criteria for burst detection objective.

• Click Skip to move to the next outlier without adjusting this one. (There are no more duration outliers, so we could also click Stop scan.)

Low frequency outlier correction

• Now select the Low freq type radio button and click Manual scan.

Nothing happens! This is because the programme cannot find a fix for the only low-frequency outlier. We have already seen that this was caused by recording drop-out, hence there are no source events from which to estimate a burst occurrence.

High frequency outlier correction

• Now select the High freq type radio button and click Manual scan.

Event 93 is centred in the main display. This is caused by a brief burst of spikes that occurs after the main burst. If you wanted to get rid of it the programme offers you two choices: you can either delete one of the events, or you can merge them together. In this case the programme is suggesting deleting the second event, because the result is closer to the trendlines in the frequency and duration graphs than deleting the other event, or merging the two events. You can change the choice by dragging the cursors to surround the other event (to delete it), or by clicking the Merge radio button. In the latter case the cursors expand to surround the two events. The caption of the action button switches between Del and Merge according to your choice.

Again, it is a matter of judgement how you proceed, but my own feeling is that since these are genuine data they should be left in the analysis.

• Click Skip until event 308 is centred.

Here the outlier is definitely caused by an artefact (which I inserted for the demonstration). The program suggests Deleting it, but the icon shows a red cross rather than a green arrow. This is because the artefact is actually very large amplitude, and the red cross just serves as a warning that you are deleting something non-trivial. However, the glitch is clearly an artefact, so:

• Click Del.

This completes the Manual scan. There are no more high-frequency outliers.

Automatic Parameter Search

DataView can perform an automatic search for reasonable off-time and on-time parameters, but you must first specify an estimated value for the average rhythm cycle period. This substantially speeds the search by enabling the program to skip parameter values that yield rhythms which have average cycle periods greater than twice or less than half this estimate. A quick inspection of the data suggests that 50 ms is a reasonable estimate, and since this happens to be the default value, no change is needed.

• Click the Search button in the right-hand Analysis panel.

The search looks for a pair of parameters that minimizes the deviation of points from the trendlines in the two graphs, frequency and duration. After a brief interval, the new parameter values appear, with a suggested minimum off-time of 6 ms, and a minimum on-time of 2 ms. DataView then automatically analyses the data with these parameters.

There are 374 bursts detected in the Rhythm channel b. There is one data-driven clear outlier in the graphs, but the others are caused by recording artefacts. If desired, you could carry out the manual outlier correction as before.

Poisson surprise analysis

The Poisson surprise method makes no assumptions about any underlying rhythm, it simply looks for bursts in which the events occur more closely together (surprisingly close) than would be expected by random chance, if we assumed a Poisson distribution of the events as a whole.

Intuitively it seems that the within-burst events in the Source channel a do occur surprisingly close together, so it should be possible to detect them with this method.

• Click the Go to start toolbar button () in the main Chart view.
• Set the Rhythm channel to c, so that we do not overwrite the bursts detected previously.
• Select the Poisson surprise mode in the Rhythm panel, and note how the right-hand panel now changes to Analysis: Poisson surprise.
• Click Analyse in the right-hand Analysis panel.

The Max in-burst interval in the Analysis panel is set at the default value 0, and with this parameter value DataView just copies the 2927 events from the Source to the Rhythm channel (a to c).

Maximum in-burst interval

The Poisson surprise method works best (and faster) if we first tell it an event interval value that is longer than any interval we could ever find within a burst. The Period histogram (bottom-right in the dialog) shows a big peak of short periods, and then a broader peak of longer periods. The latter represent the period (interval) between bursts, while the former represent the brief periods within bursts.

• Check the Log Y box above the histogram to emphasize the distinction in period durations.
• Set the Max in burst interval value to 20, and note that the red cursor now lies between the two period peaks in the histogram.
  You could also have dragged the cursor to set the value, but visual inspection of the main Chart view shows that the intervals within bursts are all considerably shorter than 20 ms.

The value chosen for this parameter should be larger than the largest interval that you would ever expect to find within a burst. It is used to break the total record into smaller more manageable chunks which can be analysed independently of each other, which substantially speeds the analysis. It is better to set the value too large than too small, but if you set it to a ridiculously large value, the whole record will be analysed in one go, which might take a very long time (or your computer might run out of memory). If you set it to too small a value, the chunk separation might occur within a burst, and the burst would thus be spuriously broken into two bursts.

Analysis surprise

Note that the default Surprise value is 2. Surprise is defined as –log10(p), where p is the probability of a set of events occurring that close together by chance. Thus a surprise value of 2 reflects a p value of 0.01 (highly significant, in statistical parlance).

• Click the Analyse button.

The frequency graph shows no high outliers, but quite a few low outliers. However, the trendline is virtually identical to that achieved previously with the Merge/drop analysis. There is one high outlier in the duration graph which is caused by the data glitch identified previously.

There are 331 bursts detected in the Rhythm channel c, which is somewhat fewer than those detected by the Merge/drop method (as reflected in the increase in low frequency outliers, indicating missing bursts). In the main Chart view you can see that events 1 - 7 match completely in event channels b and c, but that event 8 in channel b is absent in channel c.

The disparity is in part because the Poisson surprise method requires a minimum of 3 close-together events in the source channel before a putative burst is recognized, and some of the real bursts are so short that they have fewer than 3 source events. However, the missing burst 8 in channel b does actually have 3 events in it, so that is not the explanation for its absence.

• Reduce the Surprise value to 1.
• Click Analyse.

We now have some high-frequency outliers, but far fewer low-frequency outliers, and event 8 in channel b is now also picked up in channel c.

• With Width selected in the Outlier analysis panel, click the Autofix button.
• In the same panel, select Low frequency and click Autofix.
• Finally, select High frequency and click Autofix.

The result is a total of 372 events in the Rhythm channel c, and only 3 significant low outliers in the frequency graph. The second (middle) outlier at event 250 is only just below the outlier bounary and is caused by a genuinely long inter-burst period. The third outlier is caused by the recording drop-out and is unfixable.

• Click on the first low outlier in the frequency graph.

The Autofix method has attempted an automatic fix of the outlier caused by the data glitch at event 150, but has not arrived at the fix that I (as a manual operator) would have chosen. However, the other automatic fixes match what I would have chosen.

Hill-valley analysis

Note that there is a stand-alone hill-valley analysis routine that can be used on both rhythmic and non-rhythmic data.

Hill-valley analysis takes a data trace as its source, rather than an event channel. It expects the trace to contain a rhythmic series of hills and valleys, like regular ripples. The tadpole data are an extracellular recording, but such data can be transformed into an appropriate form as follows:

• Select the Transform: De-mean/median, rectify, smooth menu command from the main view menu to activate the Multi-Process Transform dialog.
• Check the De-mean/median, Rectify about 0 mV, and Smooth selection boxes.
• Enter 4 (ms) into the Half-window Time box.
• Increase the Iterations to 4.
  Multiple iterations turns plain moving average (boxcar) smoothing into approximate Gaussian smoothing, but the process runs much faster than regular Gaussian smoothing.
• Uncheck the Write new file box.
• Click OK.
• When the dialog dismisses, control-click the Autoscale toolbar button () in the main view to optimise the display.

You should now see a “hill-and-valley” trace below the extracellular recording, where each hill reflects a burst in the main recording. Note that the height of the hill reflects the intensity of the burst, but that the width of the hill does not clearly demarcate the width of the burst.

• In the Rhythm Analysis Helper dialog, select the Hill-valley analysis mode.
• Set the Rhythm channel to d.
• Advance the Trace in the Analysis: Hill-valley frame to 2 (the new trace).
• Click Analyse.

The frequency graph shows some evidence of the main trendline, but there is a cloud of high-frequency outliers. Clicking points within this cloud shows most outliers are caused by very small hills (molehills) between the main peaks (these actually provide evidence of out-of-phase activity in the recording).

We can exclude these molehills as follows.

Exclude molehills

• Select the Hill-valley ht option from the drop-down list above the histogram.
• Check the Show histogram box in the Analysis frame.

You should now see a histogram with a clear bi-modal shape. The large peak of low values at the left reflects the molehills, while the broader peak in the middle reflects the higher hills (the ones of interest).

• Set the Molehill threshold to 20 and note that the red cursor in the histogram moves just to the right of the big peak at the left. (You could have dragged the cursor, but that is less accurate.)

The molehill threshold means that any hill whose peak height above the highest surrounding valley is less than 20 gets merged with an adjacent peak. Molehills on the rising slope of a larger peak get merged with following peak  (i.e. the one later in time, to the right), while molehills on the falling slope of a larger peak get merged with the preceding peak.

• Click the Analyse button again.

The result is a total of 374 events in the Rhythm channel d, which is the same number as achieved with the Merge/drop filter. The frequency graph is very clean, with few outliers. The close pair of high-frequency outliers comes from the interference glitch we have seen with the other methods. The first low-frequency outlier is a genuine low frequency episode in the rhythm, but the other is caused by the large positive artefact we saw earlier, which produces a spurious hill. Interestingly, the width outlier comes from the flat-line drop-out. This generates a hill because the drop-out voltage is below the mean voltage of the recording, and so after de-meaning it produces a voltage offset which is picked up by the smoothing process.

Comparison

The results of these different modes of analysis are virtually identical in terms of frequency.

• Un-checking the Autoscl box above the frequency graph.
• Set the top axis scale to 30 and the bottom axis scale to 10.
• Switch the rhythm channel between b, c and d. The trendline and data points in the frequency graph hardly shift at all.

The burst duration results are rather different. In general the Poisson surprise method results in slightly shorter bursts than the merge/drop filter, although the difference is not great. This is partly because the former requires that each burst should derive from at least 3 source events, while the latter does not.

The burst durations detected hill-valley analysis have a more complex relationship to the underlying burst duration, because the averaging process blurs the edges of the burst. But on the other hand, the peak data value of the smoothed trace within the rhythm event gives an indication of the intensity of the burst. This could be visualized separately in a histogram or scattergraph.

 

---